Adatbázis tárgyra jegyzetek

Kreditumok

Felhasznált irodalom:

• Gajdos Sándor – Adatbázisok (2019)
• Gajdos Sándor – Előadások
• https://vik.wiki/images/c/cb/Adatbazisok_jegyzet_2022_v2.pdf
• Wikipédia az adatbázisokról és adatmodellekről
• https://vik.wiki/images/c/cf/Lagyszamitas_jegyzet_2011_fuzzy.pdf
• Lábjegyzékek: Dragonyos

Köszönet a diagramok és kiegészítőkért Toma066-nak.

Adatbázis kezelők felépítése

Alapfogalmak

Adat: Nem értelmezett, de értelmezhető darabja a valóságnak.
Példa: 21, nincs megmondva, hogy ez egy életkor vagy, hogy milyen számrendszerbe kell értelmezni.

Információ: Értelmezett adat.
Példa: 21 életkor.

Tudás: Kontextusba helyezett információ. Pl: Potenciális vásárlók a 42-es cipőméretre.

metaadat: Adat adata. (vagy adatot leíró információ)

Szintaxis: Adatok ábrázolási módja. Pl: a 30-at 10-es számrendszerbe értjük.

Szemantika: Egy adat jelentése. Pl: a 42 egy életkor.

Struktúrált adat: Olyan adat, ahol a szintaxis megegyezik a szemantikával.

Struktúrális metaadat: Pl: adattípusok, oszlopnevek, táblanevek, adatméretek. Szemantikus metaadat: Pl: hozzárendelt értelem, pl: egy adott táblának milyen attribútumai vannak, vagy pl a kapcsolatok kardinalitása

Szemistruktúrált adat: Olyan adat, ahol a szintaxis nem egyezik a szemantikával. Pl: JSON, XML. Oké, ez semmit nem mond, ezt úgy kell érteni, hogy olyan adat, amelyet előre meghatározott formában (pl. táblázat, adatbázis mezők) tárolunk, tehát maga a szerkezete már sokat "magyaráz" belőle.

Nemstruktúrált adat: Nincs szemantika, így nincs szerkezete sem. Pl: Bitstream, kép, videó. (Ezeknek is van de most hagyjuk)

Séma: Adatbázis fogalmi váza, más néven struktúrája. Más szóval: milyen adatok milyen formában tárolódnak az adatbázisban. Az üres halmaznak / adatbázisnak is van sémája.

Adatbázis kezelő rendszerek (DBMS) Database Management System

Adatbázis: A valós világ részhalmazának leírásához használt adatok összefüggő, rendezett halmaza. Példa: Lehet az SQL is adatbázis, de definició szerint az Excel is az.

→: Következés.

Adatbázis-kezelő rendszer:
Külső séma: A nézetekhez tartozó sémákat gyakran külső sémának (external schema) is nevezik.

Data Manipulation Language: kérések megfogalmazása, értelmezése.

Data Definition Language: megfogalmazhatjuk, hogy milyen adatokat milyen formában tárolunk.

Database manager: Ellátja fordított séma alapján a lekérdezéseket, adatvédelmet, szinkronizációt és az integritásra figyel. Sémafordító: Értelmeti az adtabázis Data Definition Language leírását és külön fordítja le.

• Hardver-szoftver rendszer
• 1 vagy több személy számára
• Magas szinten - Felhasználó anélkül tudja elvégezni a feladatait, hogy tudná a háttér DBMS működéseket.
• Lehetővé teszi az adatok olvasását, módosítását.

Tulajdonságok:

• Nagy adatmennyiség
• Gazdag struktúra: Rekordok között logikai kapcsolat hozható létre, amit lehet arra is használni, hogy a műveleteket felgyorsítsa.
• Hosszú életciklus: Pl: Népességi adatbázis, hosszú ideig fent kell maradni, sok technikai váltást túl kell élnie.

Tárolás manapság:

• Mágnesszalag (inkább már nem)
• HDD
• SSD

Programozói/ felhasználói szemlélet

Klasszikus adatbázis rendszerek 2 fázisa:

• majdani adatok tárolási rendje ~ támogató: DDL3
  • séma megteremtése
  • adatai: technikai metaadatok, adatbázis különösen védett részébe kerülnek.
  • ^- elvesztésük/sérülésük miatt az adatbázis elérhetetlen lesz
• adatok tárolása, lekérdezése ~ támogató: DML5
  • Lekérdezések önálló programként, alkalmazásként is működnek
  • speciális adatbázis-lekérdező nyelven (pl. SQL) kérdéseket fogalmaz meg (valaki)
  • Lekérdezés feldolgozó értelmezi, optimalizálás is szükséges: egy esethez több úton keresztül is el tudunk jutni.
  • adatbázis-kezelő válaszol
  • lekérdezés-feldolgozó alakítja értelmezhető formába a DB-manager számára → ilyenkor optimalizál is.

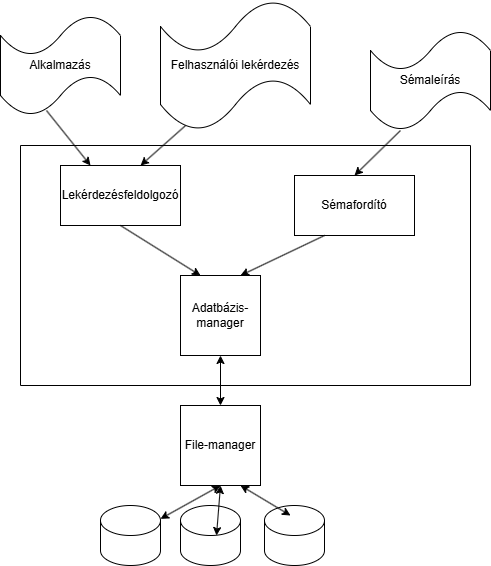DDL és DML gyakran egy egységes nyelvként dolgoznak: pl. SQL.
Állománykezelő biztosítja a hozzáférést a fizikai adatbázishoz → + szoros kapcsolatban az OS-szel.

DBM járulékos feladatai

• Adatvédelem (privacy)
  • Különböző hozzáférési módok vannak.
  • Jelszóhoz is köthető a hozzáférés vagy célhardver is védheti az adatokat.
• integritás (integrity) (ellentmondásmentesség)
  • olyan szolgáltatás, mely a DB adatainak helyességét ellenőrzi a beszúrás, törlés, módosítás kényesek a sikeres végrehatjást.
  • DB logikai felépítése is segíthet ezen
  • típusai:
    • Formai ellenőrzés: adott mezőben valóban az engedélyezett érték áll-e. Pl: Ne hagyjunk 999-at az életkornál.
    • Referenciális integritás: egyik helyről kiolvasott adatelemnek meg kell egyeznie más helyről kiolvasott adatelemmel. Példa: Ha 2 ugyanolyan lekérdezést végrehajtottunk egy táblán, anélkül, hogy az módosult volna, azoknak ugyanazt az eredményt kell visszaadniuk.
    • Strukturális integritás: Nem sérült-e a feltételezés, amelyre az DB-t építettük. Gyakori hiba: egyértelműség megszűnése. Pl: Araboknál férfiaknál lehet több feleség is, máshol ez nem egyértelmű. Vagy adatbáziskényszerek, mely miatt az adatok kapcsolatban vannak. Olykor ez egyértelmű, olykor nem. Utóbbiak közé tartoznak a függőségek, amikor egyes adatbázisértékek meghatároznak más értékeket.
• Adatbiztonság (security): adatok védelme érdekében, hogy se szoftveres/hardveres hiba esetén se vesszenek el: naplózás, rendszeres mentés, kettőzött adatállomány, elosztott működés
• Szinkronitás (synchronization): mai DB-k már többfelhasználósak + tranzakciókezelés:
  • adatokon egyidőben végzett műveletek ne tegyenek keresztbe egymásnak
  • ez biztosítja ezt pl. zárak (locks) segítségével

Adatbázis-kezelők felépítése

• Rétegmodell
  • lényege: probléma több részre bontása, részek épüljenek egymásra, minél kisebb felületen érintkezzenek
  • rétegek egymástól függetlenül megváltoztathatóak legyenek
  • a rétegek közötti interface változatlan marad → adatfüggetlenség
    • Fizikai adatfüggetlenség (Eszközfüggetlenség): fizikai szinten véghez vitt változások nem érintik a logikai DB-t, → az adathordozó fizikailag kicserélhető (Pl: fizikai meghibásodás, technikai fejlődés), anélkül, hogy bármilyen változás lenne a logikai részben. (Tehát nem látunk változást pl. a rendszer teljesítőképességében.)
    • Logikai adatfüggetlenség: logikai DB megváltozása nem jár nézetek megváltozásával → nem mindig teljesül
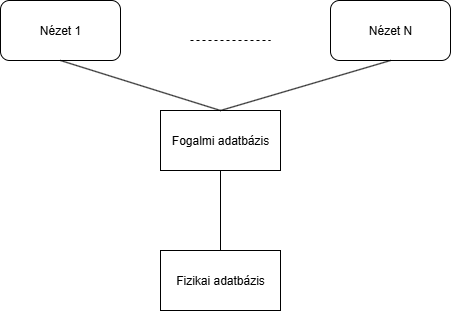
  • Rétegmodellhez példa: 3 rétegű modell: rétegek egymástól függetlenül külön változtathatóak. (Fizika, Logika, View)
  • Fizikai adatbázis: itt valósul meg az adatok fizikai tárolás, Pl: adatstruktúrák, amelyekben megvalósul az adattárolás.
  • Fogalmi adatbázis (logikai): való világ egy darabjának leképzése, adatok értelmezése, ehhez tartozó séma: fogalmi séma.
  • Nézet (View): felhasználó az adatbázisból lát, több felhasználási lehetőség → több nézet, ehhez tartozó séma: külső séma. Fontos, hogy ez csak származtatja az adatokat.
• Felhasználótípusok
  • Képzetlen felhasználó: nem ért az adatbázisokhoz, se a nyelvükön.
  • Alkalmazásprogramozó: felhasználói program írása
  • Adatbázis admin: jogosultságok, mentés, visszaállítás
  • DBMS tervező/programozó: Specialista, tudja, hogyan kell adatbázisrendszereket tervezni és csinálni.

Az adatbáziskezelők általános statikus 7 rétegű modellje (környezetét is figyelembe véve): Relációs séma: Egy értelmezés, amit egy objektumra ráhúzva jelentést kapunk. Pl: 100 bitre: Ember séma: 1. 20 bit ember életkora, 2. 80 bit pedig a neve. Adatbázis séma: Ha egy adatbázis több relációs sémát is tartalmaz, akkor a relációs sémák összességének neve adatbázis séma.

A fogalmi (logikai) adatbázis és ER modellek (vagy EK modellek)

Ismétlés: Az adatbázis rendszer jól struktúrált adat tárolására alkalmas.
Arra szolgál, hogy a tudást le tudjuk képezni adattá, és azt mások minnél hatékonyabban vissza tudják tudássá alakítani.
(Tudás=>adat=>Tudás).

Adatmodellezés

Adatmodell: Olyan formális rendszer, ami jellemzi az adatokat és relációikat, és definiál egy művelethalmazt, amivel az adatokat elérni és módosítani lehet.

Formális: Egy objektum akkor formális, ha annak a jellemzésére egy jól meghatározott szimbólumrendszert használunk. +megmondjuk, hogy a szimbólumok mire valók a rendszeren belül és a rendszerben szabályokat definiálunk, amiket a műveletekkel nem szegünk meg.

Egy formális jelölés rendszer: Entity-Relationship (ER vagy EK) modell.
A modell az adatokról így kell kinéznie: (Ezeknek meg kell felelnie)

• Elemek tartós tárolása,
• Jól struktúrált adatok tárolására alkalmas,
• Halmazokat használunk a modellben,

Ez egy ER modell, ha különböző kapcsolat-,tulajdonság- és egyedhalmazunk van.

Tulajdonság: lesz az az attribútum, ami egy egyedet jól tud jellemezni és egyediséget ad neki. Pl: Adóazonosító jel

Egyed: Valami egyed, ha saját léte van. A saját létet a tulajdonsága(i) alapján kapja.

Példa: Az egyed, tulajdonság-ra:

Név	Életkor	Lábméret
Ferenc József	42	43

Itt a "Név","Életkor","Lábméret" mind tulajdonság. A sor, amiben az adatok vannak, pedig az egyed.

Ezek az adatok addíg tudnak egyedeket egyedi módon leírni, amíg nincs 2 ugyanolyan nevű, korú és lábméretű ember.
Példa: Szeretnénk 100000000 hangyából egyedeket csinálni. Ezt úgy lehet, hogy minden hangyához rakunk egy azonosító számot. (Vagy minden hangyát egy számozott dobozba rakjuk az összeset külön-külön):

Hangya azonosító
1
2
31
791

Halmaz: [A matematikai halmaz] +, hogy a benne található elemeket meg tudjuk különböztetni egymástól.

Kapcsolat: Egyedeknek a viszonya.

Jól struktúrált adatoknál 1 halmazba kell rakni, ha közös az értelmezés és az attribútumok hasonlóak. Pl: A név táblába, a NÉV mező mindenhol az ember egyed nevét tárolja.
Halmaz példák:

NÉV
Jakab
Józsi
Feri
Máté

ÉLETKOR
17
8
99
31

Látható, hogy egy halmazba azonos értelmezésű objektumokat tárolunk, hogy a szemantikus metaadatok közösek lehessenek. (Majd ezekből fel kell építeni a kapcsolat példányokat (Pl: SELECT result)) Példa tulajdonság halmazra:

Valami SZÍNE
Kék
Piros
Zöld
Cyán

Ezeket tárolhatjuk, Pl: 15 hosszú karakterláncként vagy r,g,b szám 3-asokként. Mindegy, csak azonos legyen a szemantika a halmazba. (Közös szemantika)
Halmaz ~= Típus de mégse, lássuk:

Halmaz név	Típus
NÉV	VARCHAR(50)

Hasonlóak. (De nem 1/1 ugyanazt jelentik)
Példa: Definiáljunk egy egyedhalmazt, a hallgatót. Ennek neve lehet Hallgató és de XN-34-CDT is, csak az előbbivel jobban járunk.

Hallgatók
Név	Kor	Cipőméret
Rontó Palkó	23	44

Ebben a tulajdonsághalmazok a Név,Kor és Cipőméret.
Csináljunk egy másik egyedhalmazt is:

Egyetemek
Név	Milyen jó
BME	Nagyon
Corvinusz	Meh

Egyedhalmaz: Azonos tulajdonsággal rendelkező egyedek halmaza.

Tulajdonsághalmaz: Azonos egyedet leíró tulajdonságok halmaza.

Kapcsolathalmaz: Azonos kapcsolathoz tartozó szemantika.

Hát, ez nagyon sokat mondó. De próbáljuk meg megmagyarázni. Példa: Legyen egy [Oda jár (X,Y)] kapcsolatunk. Ahol mondhatjuk ezt is: [Oda jár (Jakab,BME)], ami azt jelenti, hogy Jakab a BME-re jár.
Lehet ternáris is a kapcsolat (akármennyi szereplő lehet benne). Példa: A postán a feladók csomagokat küldenek a címzetteknek. Itt van a feladó, a csomag és a címzett is. Ezekből lehet a [Posta] reláció példányokat csinálni, amik a kapcsolathalmazba tartoznak.
Fontos, hogy ternáris vagy többes kapcsolat esetén sosem szabad egy kapcsolt egyedet sem ignorálni Pl: csak 2 egyed kapcsolódik érdemben. Nem lehet csak 2-t használni, ha 3 van.

Relációs sémákra példa

Tegyük fel, hogy akarunk modellezni egy olyan modellt, ahol tároljuk, hogy ki jár oda. Egy diák egy helyre tud járni és egy iskolába többen is járhatnak. Az iskolákat a neve egyedileg megkülönbözteti, ezen kívűl tároljuk az alapítás évét. A tanulóról a nevét, igazolványszámát (ami egyedi) és életkorát tároljuk. Ezen felül a kapcsolatba tároljuk, hogy mikor kezdett el oda járni.

Ez alapján egy relációs séma, amit adhatunk, így nézhet ki:

TANULO( igazolvany_szam, nev, szuletesi_datum)
IDE_JAR(tanulo_igazolvany_szama, iskola_neve, mikortol)
ISKOLA(nev, alapitas_eve)

No, ebből sok minden látszik. Elsőnek feltűnhet, hogy itt a relációt is táblaként modelleztük, viszont a relációt az attribútumai nem azonosítják egyedileg. Ezt meg kell oldani. Ezen felül még látszik, hogy formális okokból nem használtunk ékezetes betűket és szóközöket az azonosítókban.

Az elsődleges kulcsokat 1 aláhúzás, az idegen kulcsokat 2 aláhúzás jelöli.
No, de mi van, ha mi spórolni szeretnénk és nem akarjuk az iskola neveket és az igazolvány számokat redundánsan 2 helyen tárolni? A megoldás a mesterséges kulcs. Ennek az a szerepe, hogy egy olyan szám, ami az attribútumoktól függetlenül egyedileg azonosítja az adott egyeded, ennek suffixa általában "_id" szokott lenni. Ez egy sima szám és így nem kell 2 helyen kulcsként a neveket / más komplexebb adatokat tárolni:

TANULO( tanulo_id, igazolvany_szam, nev, szuletesi_datum)
IDE_JAR(ide_jaras_id, tanulo_igazolvany_szama, iskola_neve, mikortol)
ISKOLA(iskola_id, nev, alapitas_eve)

Fontos látni, hogy a kapcsolat is kapot egy mesterséges kulcsot így már azt is lehet egyedileg azonosítani. Azt is fontos észrevenni, hogy attól még, hogy nem jelöljük az egyedi attribútumokat, majd leképezésnél nem szabad engedni, hogy 2 ugyanolyan igazolványszámú tanuló legyen. Erre majd a constraint-ok lesznek hasznosak.

ER modellek a valós életben

Példa: Az SAP rendszerbe nagyságrendileg 10000 egyedhalmaz / kapcsolat halmaz található. Ennek a fejben "elképzelése" nagyon nehéz és nem igazán elérhető.

Erre találták ki az ER diagrammot.

ER diagram: Egy ER modellt grafikusan ábrázoló diagram. Jelzések:

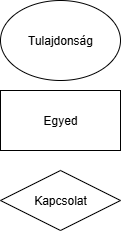
EER (Extended ER ) model: Az extended ER olyan speciális funkciók megvalósítására szolgál, amire az ER nem képes. Elemei az ISA kapcsolat, gyenge egyedhalmaz és a determináló kapcsolat.

Ábrázoljuk az előző hallgató és egyetem ER modellt ER diagramként:
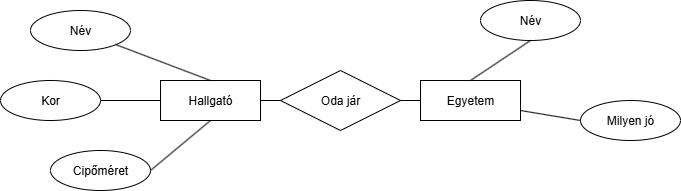Itt a krumplikba vannak a tulajdonsághalmazok és össze vannak azzal kötve, hogy minek a tulajdonságai.
Az oda jár reláció is meg van jelenítve a 2 halmaz között.
De tudjuk-e az egyedeinket (és így a relációinkat) jól megkülönböztetni?

Kulcs: Olyan tulajdonságok, értékek, ami egy egyedet egyértelműen azonosítani képes. Jelölés:

Idegen kulcs: Egy olyan mező, ami egy kapcsolaton keresztül lehetővé teszi az egyik egyednek, hogy a másik kapcsolt egyedet azonosítsa. Ilyet nem jelölünk az ER modellben. Ezt relációval jelezzük.

Az egyetem nevét választhatjuk kulcsnak, mert 2 BME nincs (Oké Bécsi és Budapesti BME is van de a teljes nevük szerint már lehet.)
Viszont a Hallgató már egy kicsit bonyolultabb...
Mit használjunk? Használhatjuk a Név-Kor-Cipőméret hármast, de az nem lenne túl jó egyedi azonosító, mert létezhet 2 ember ugyanazzal a névvel, lábmérettel és korral.
Megoldás: Csináljuk ugyanazt, mint a hangyákkal, minden ember kap egy egyedi számot (ID-t):
Az egyetemnél bejelöltük a Nevet kulcsnak mert az megfelel annak.
No, de nem csak 1 reláció lehet 2 (vagy N) egyed között:
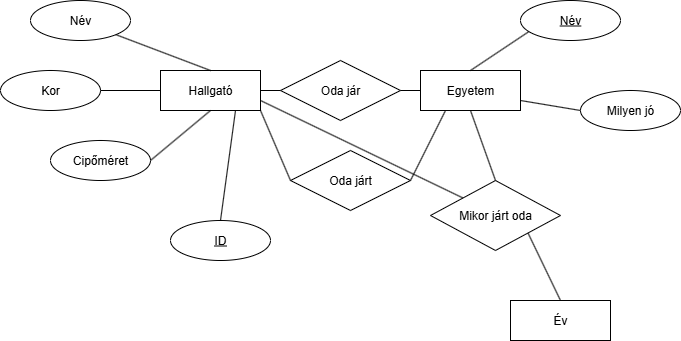Lehet, hogy akarjuk tudni, hogy ki járt RÉGEBBEN ide. Vagy, hogy ki melyik évben járt ide.
Fontos, hogy mit tudsz használni kulcsnak, milyen relációid lehetnek, az függ az aktuális DBMS rendszertől.

Kapcsolatok funkcionalitása (/kardinalitása)

A kapcsolat halmazok funkcionalitását csak bináris kapcsolatra értelmezzük.
Kapcsolat típusok:

• 1 az 1-hez:
  TFH: Egyed1 oldaláról 1-N-nél. N legfeljebb 1 és Egyed2 oldaláról pedig 1-M-nél M legfeljebb 1. Ebből N legfeljebb 1 és M legfeljebb 1 → 1-1-hez reláció.
  Ez a reláció felesleges, hatékonyság miatt a 2 egyed egybe is lehetne. És nem annyira tudunk példányszintent relációt csinálni, mert nem tudjuk, hogy milyen példányok lesznek. Csak az Egyedek struktúráját ismerjük.
  Az 1 az 1-hez kapcsolat invertálható, mert mind kettő oldalról egyértelmű a leképezés.
• 1 a több-höz:
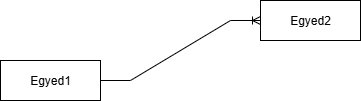  Ez a reláció az egyik oldalról egyértelmű, a másikról pedig nem egyértelmű. (1-több-höz = több-1-hez)
• több a több-höz:
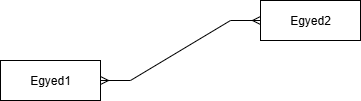  Ez a reláció az egyik oldalról sem egyértelmű.
  Itt majd problémákba ütközünk, kell normalizálás de erről majd később.

Fontos: Itt a pontos ER modelling jelölést használtam, de van, ahol nyilakkal kell jelölni a relációkat. (Pl: Az Adatb tárgyban nyilazunk). Azt kell tudni, hogy mindíg az 1-es kapcsolat felé mutatjuk a nyílat. 1 a többhöz esetén az egy felé. 1 az 1-hez esetén mind kettő fele. Pl: Ha nem tudod, hogy merre nyilazz kérdezd meg a gyanusított egyedet (amiből feltételezed, hogy kell húzni) és tedd fel a kérdést: "Ki/Mi tartozik hozzá". Pl: Ha feltételezzük, hogy 1 filmet csak 1 író írhat de 1 író több filmet is írhat. Így a válasz az írónál, hogy "Ehhez az íróhoz ezek a filmek tartoznak."

X is a Y kapcsolat

Modellezzük le egy repülőtéren dolgozók nyilvántartóját: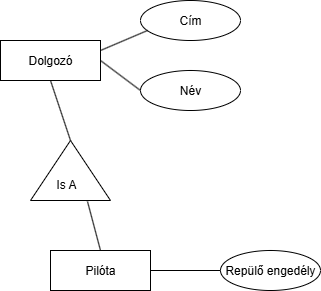
Azt akarjuk, hogy a repülőengedélyt ne kelljen a dolgozók egyedbe tárolni. Megoldás: Csinálunk egy Pilóta egyedet és hozzá kapcsoljuk a Dolgozóhoz. Az [Is A] reláció azlap jelentése: X is a Y, szóval Példa: Pilóta egy Dolgozó. Mindíg abból mutat nyíl feje, ami leszármozik. (Ez kicsit olyan, mint az Object-Oriented inheritance).

Gyenge egyed halmaz

Példa: Az összes budapesti általános iskola összes osztályát ki akarjuk listázni. Így kapunk valami ilyesmit:

Osztályok
1.A
2.A
1.A
1.B
1.B
1.B
2.A
...

No, ez így nem jó. Az a probléma, hogy iskola szinten egyediek az osztályok, de sok iskola szinten már nem.

Gyenge egyedhalmaz: Egy olyan halmaz, ahol az egyediség nem mindíg van biztosítva. Más szóval: Amikor nem egyértelműen azonosítható (más egyedhalmazra is van szükség). Jelölés:

Determináló kapcsolat: Egy olyan kapcsolat, ami egyediséget biztosít egy gyenge egyedhalmaznak. Más szóval: A gyenge egyedhalmazt köti össze a tulajdonos egyedhalmazzal. Jelölés:

Függvényszerű bináris kapcsolat: Függvényszerű egy bináris kapcsolat egy az egyhez kapcsolat esetén. Példa ezekre (az iskolás példát használva):
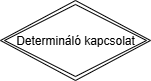
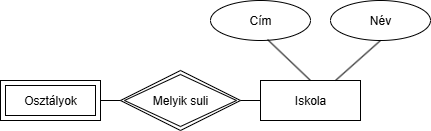Az osztályok az által lesznek azonosítva, hogy melyik iskolához tartoznak. Most nézzünk egy példa outputot:

Osztályok
Kossuth Általános Iskola - 1.A
Ezüst Általános Iskola - 2.A
Kossuth Általános Iskola - 2.A
Ezüst Általános Iskola - 1.A
...

Mostmár az egyediség biztosítva van.

Adatmodellek

A Chen féle ER modellhez kell hozzárakni valami +-t is, hogy adatmodellnek lehessen hívni azt.

Az adatmodellek megjelenési sorrendben:

1. hierarchikus
2. hálós
3. relációs
4. objektumorientált
5. deduktív
6. fuzzy

A relációs adatmodell a legelterjedtebb.

Relációs adatmodell: A halmazok valahogy reláció-ban vannak egymással.

Reláció: Halmazok descartes szorzatának részhalmaza.

Reláció fokszáma: A relációban lévő oszlopok (attribútumok, tartományok, tulajdonságok) száma a reláció foka (arity, aritás).

Példa:
Legyen D1 és D2 halmaz:

D1
1	2	3

D2
a	b

D1 és D2 szorzatának részhalmaza:

D1 x D2
1	a
1	b
2	a
2	b
3	a
3	b

De nem kell ez a teljes, lehet kisebb részhalmaza, pl legyen r1 reláció:

r1
1	a
3	b

Ez is reláció. (Az üres halmaz is reláció, abban is olyan elemek lennének amiben érték párok vannak). Ha elnevezzük az oszolopokat:

D1	D2
1	a
3	b

Akkor már lehet tudni, hogy melyik adat melyik halmazból van.
Ez is egy formalizmus.

A relációs adatmodell, V2

A tudás replezenetálására kell, hogy tárolni lehessen az adatokat. (Entitások, tulajdonságok, relációk), fontos a viszony.
Jól struktúrált adatokat jól körbe írtunk már struktúrális metaadatokkal. Ezekhez az oszlopokhoz hozzárendelve a szemantikát, értelmet kapunk.
Ötlet: Az összetartozó rekordokat össze pointerezzük. Ez nem telljesen jó, de ez is egy megoldás.
Pl: Ha bizonyos adatokat össze pointerezünk akkor az egy rugalmatlan reláció lesz és oda-vissza nem lesz egyértelmű az összekapcsolás.
Másik ötlet: Hol van 2 olyan adat, ahol 2 hasonló érték van. -> Érték azonosság alapján kapcsolunk össze adatokat.
A relációs adatmodell értékazonosságon alapul.

Értékazonosság: 2 érték azonos, ha attribútumai szerint hasonlóak.

Műveletek az adatokon

50 évvel ezelőtt: Minek lenne értelme? (Táblázataink vannak és abba adatok és értelmes dolgokat akarunk lekérdezni).
Kérdés, minek kell definiálni?
A definició alapján a halmazműveleteket kell definiálni:

• Halmazalgebrai relációk: unió, metszet, stb... BIZTOS kellenek!
• Új relációk is fontosak: vetítés, szelekció... majd többet lejebb tudhatsz meg.

Relációalgebra: A relációhalmazon végzett műveletek.

Reláció unió: 2 relációt összecsatolunk és a duplikáns elemeket kiszedjük, hogy csak egyszer szerepeljenek. (Van-e értelme?) Példa: Adott egy 6 és egy 3 oszlopú reláció. Uniózzuk össze ezt! Hogy kéne ezt csinálni? Az eredményhalmazban levő oszlopoknak nem biztos, hogy lesz értelme.
Ötlet: Azonos parítású relációkra értelmezett az unió műveletét engedjük CSAK. Egy adatot, meg csak akkor tegyünk az unióba, ha már nincs is benne.
Miért gáz a duplikáns adat: Azért, mert az ER modellnek csak akkor van értelme, ha mindenki egyedileg meg van különböztetve. Ha csak az egyiket módosítjuk, akkor már baj van.
Hacky megoldás: Új rejtett oszlop (row_id), ami egyediséget ad egy sornak.

Parítás: 2 relációnak akkor azonos a parítása, ha azonos oszlopszáma van.

Gyakorlatban: Az a jó megoldás, ami működik.
Lényeg: legyen egy formalizmus, ami alapján az adatbázissal interaktálhatunk.

Reláció különbsége: 2 reláció különbsége azonos parítású relációkra értelmezett és végrehajt rejtuk egy halmaz különbséget.

Reláció metszete: 2 reláción való metszet halmazműveletként vétele.

Komplemens képzésnek mennyi értelme van? Nem sok, mert kis adatbázis rekordok komplementere baromi nagy.

Véges relációk: Ha az input és tároló kapacitás véges és a végeredményhalmaz is véges, akkor ezeket láncolni lehet. Véges relációkból mindíg csak véges és zárt relációkat szabad előállítani).

Descartes szorzat: A Descartes szorzat vagy kereszt szorzat 2 halmazt össze lehet kapcsolni az össze elemen keresztül.

Lehet-e, hogy van olyan eset, ahol a descartes szorzatot nem érdemes alkalmazni? Nem, nincs ilyen. (Tipik, triviális vizsgakérdés) Ez a szorzat mindenfélére jó lesz.
Lehet olyat csinálni, PL: minden hallgató minden egyetemmel össze van kapcsolva és mi majd kiválogatjuk, hogy melyik relációk kellenek. Pl: ide jár.

Relációs schéma: egytábla oszlopainak attribútumai, neve, típusa, stb...

Projekció: Jele: Π. Relációs schémából fog kiválasztani valamilyen elemeket attribútumok szerint.

Példa konkrét reláció halmazra:

Név	Mennyit keres
Feri	5 FT
Jani	999999999 FT

Példa: Egy projekció ami kiírja azt, hogy ki mennyit keres: Πnev,kereset(emberek)

Szelekció: 1 operandusos művelet. Adott halmazból bizonyos attribútum alapján. Jele: σ. Az operandus reláció azon elemeit őrzi meg, melyen az input kritérium formula igaz értéket ad.

0-ad rendűformula: Egy formula nulladrendű ha nincsenek benne kvantorok.

Példa: keressük meg azokat az embereket akik 600 FT-kevesebbet keresnek: Πnév, σ(<600 FT), Példa: output:

Név
Feri

Relációs teljes: Ha egy relációsalgebra ezt az 5 műveletet ki tudja fejezni, akkor relációsan teljes.

(EXTRA!) Objektumorientált adatmodell

Az objektumorientált adatmodell az objektumorientált programozás módszertanának egy része.
Hatékonyságában nem olyan jó még, mint a relációs adatmodell.

Objektum: Az objektumorientált adatmodellben jelenik meg. Ez az objektum egy olyan egyed, ami tudja a belső tulajdonságait, és azt, hogy milyen másik objektumokkal van relációban.

Objektumorientált: Az objektumorientált adatmodellben az adatbáziselemek tudják, hogy kik-ők, mik-ők? Egyedek helyett objektum elemek vannak.

Az objektumorientált adatmodell főbb jellemzői:

• Becsomagolás: (angolul: encapsulation) Az objektum adatainak és rajtuk végezhető műveletek (metódusainak) összessége egy halmazban.
• Adat absztrakció: Az adatokat absztrakt módon is meg lehet határozni és ábrázolni.
• Öröklődés (inheritance): A szülő objektumból a leszármazottjaik öröklik a műveleteiket és tulajdonságaikat.
• Többalakúság (polymorphism): Ugyanazt az utasítást / műveletek más objektumok eltérően értelmezik.

(EXTRA!) Hierarchikus adatmodell

Ez az adatmodell volt az egyik első, és egyben az egyik legkorlátozottabb, sok szabállyal. A hatvanas évek végén alakúlt ki. Pl: BM IMS adatbáziskezelő rendszer alkalmazta ezt a modellt.
A nevéből is látható, hogy hierarchikusan, fa szerkezetben lesznek a modellek elhelyezve.

Példa: Hierarchikus adatmodellre:

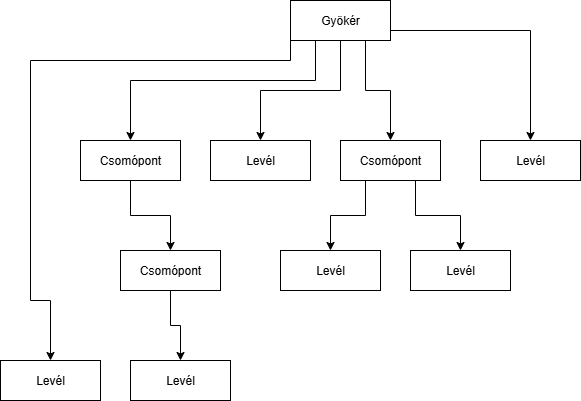
Hierarchikus: Az adatmodell hierarchikus, ha az adatok és kapcsolataik véges mennyíségű fával írhatóak le és nincs benne több a többeshez reláció.

Definició szerint több egymástól független fából is állhat egy modell.
A fák csomópontjaiban és leveleiben helyezkednek el az adatok.
A közöttük lévő reláció a szülő-gyerek kapcsolatot jelenti.
Csak 1 a többhöz kapcsolat megengedett, ez azt jelenti, hogy 1 szülőnek több gyereke is lehet, de egy gyereknek csak 1 szülője lehet. Példa: jó példa lehet egy családfa, vagy egy főnök-beosztott kapcsolat:

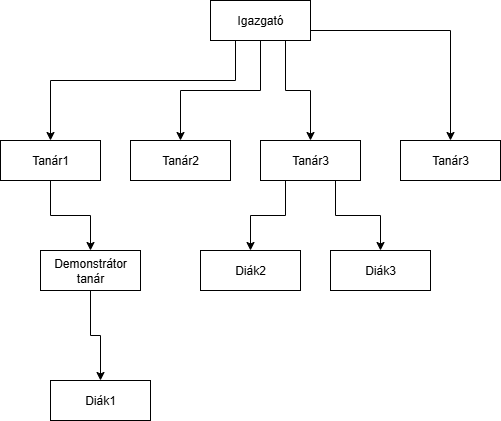
(EXTRA!) Hálós adatmodell

A hálós adatmodell egy hierarchikus adatmodell továbfejlesztett része.
Elsődlegesen azért csinálták, hogy a bonyolultabb relációkat jobban tudják ábrázolni.
1969-ben a CODASYL bizottság által létrehozott DBTG (Data Base Task Group) jelentése alapján hozták létre.
Megjelenése után 20 éven keresztül majdnem mindenhol csak ezt használták. Utána a relációs adatmodellles adatbázis elverte népszerűségben.

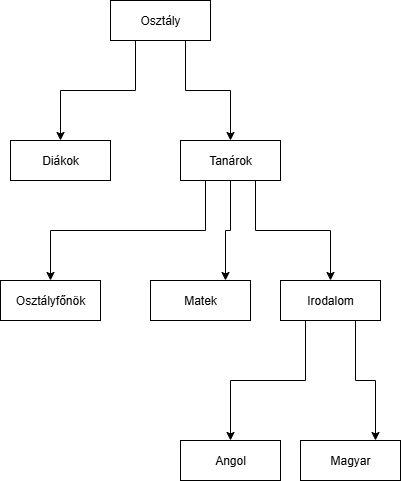Példa a hálós adatmodellre: A hierarchikus adatmodellhez képest itt már nem csak egy szülőhöz tartozhat több gyerek, de egy gyereknek is lehet több szülője. Az egyedek között tetszőleges kapcsolatok építhetők ki. Ez a bizonyos háló tetszőlegesen nagy méretű lehet, ábrázolása több, egymásra hierarchikusan felépülő kisebb egységekkel, setekkel történik.
A hálós adatmodellek gráffal írhatóak le.
Példa: A több ősre:

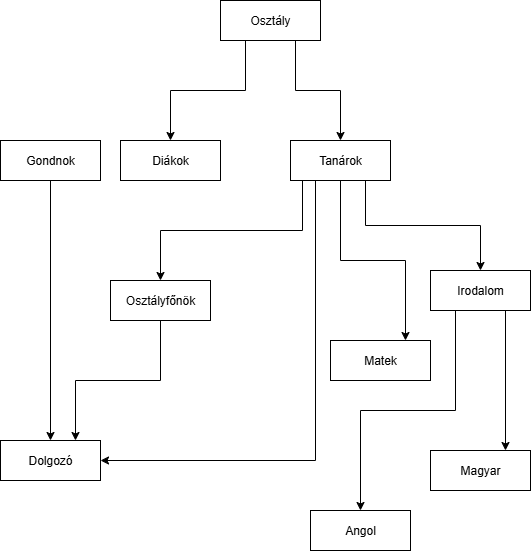
Hálós: Egy adatmodell hálós, ha gráfként lehet ábrázolni az egyedek relációját.

Hálós reláció: A hálós reláció, vagy set a hálós modellben rekordtípusok közötti kapcsolatot írja le. Formálisan: Kétszintű fa amelynek gyökéreleme a tulajdonos, és levélelemei a tagok.

Tárolási terület: A tárolási terület, avagy area egy hálós adatmodellben egy fizikai tárolási egységet jelöl. Valamilyen szempontból egységesen kezelendő adatfájl.

Ezzel a kettő új definició segítségével a legbonyolultabb hálós modellek is leírhatóak.

(EXTRA!) Deduktív adatmodell

A deduktív adatmodell a relációs adatmodellre épül és azt kiterjeszti logikai következtetésekkel.

Deduktív: Egy adatmodell deduktív, ha a reláció halmazokban csak tények vannak tárolva és szabályok segítségével nyernek ezek a relációk értelmet.

Szabály: Logikai formula.

Ez azért jó, mert új szabályokat tudunk deduktálni, anélkül, hogy eltárolnánk azokat, mert a tényeg és szabályok már megvannak. Példa: Tényekre:

• Anna egy diák.
• Péter egy tanár.
• Péter tanítja Annát.

Példa: Szabályokra (Prolog formátumban):
jarhat_kurzusra(X, Y) :- diak(X), tanit(Tanar, Y).
Aztán szeretnénk tudni, járhat-e kurzusra valaki:
?- jarhat_kurzusra(peter, Programozás).

(EXTRA!) Fuzzy adatmodell

Kezdjük egyből egy paradoxonnal.

Példa: Van egy homok kupacunk és valamennyiszer elveszünk egy homokszemet belőle. Minden homokszem elvételekor ugyanúgy homokkupac marad a homokkupac. Ebből azt tudjuk következetni, hogy:
Homokkupac - 1*homokszem = Homokkupac
Ebből az egyenletből észre vehetjük, hogy csak akkor lehet igaz, ha a homokszem=0, ha a Homokkupac mérete véges. Ezt csak azért tudtuk fuzzy logikával megállapítani, mert nem volt pontosan a homokkupac és homokszem definiálva.
Ahhoz, hogy ne legyen paradoxon, kell egy formális definició a Homokkupacnak. Példa: "A homokkupac definíciója legyen az, hogy a homokszem halmaz elemszáma legalább négy és az elrendezés legyen tetraéderszerű."

Fuzzy: A fuzzy adatmodell a bizonytalan vagy pontatlan adatokat és relációkat is képes kezelni. Az értelmezésükhöz tagsági fokokat (0 és 1 közötti értékeket) rendel, amelyek kifejezik, hogy egy állítás mennyire igaz az ismert adatok alapján.

Röviden a fuzzy adatmodell úgy fok működni, hogy fuzzy logikával meghatározza a relációkat, azok értelmét, de ide majd töltök fel még extra anyagot.
De vajon tényleg szükségszerű-e, hogy a rendszerünk csak ilyen definíciókat kezelhessen?

Fuzzyness - hoszabb felvezetés

Nyilván vannak olyan kupacok, amikre ránézve mindenki tudja, hogy azok homokkupacok, és vannak olyanok amiről mindenki tudja, hogy nem azok semmi körülmény alatt. Sajnos vannak azok is amik csak "valahány %-ban homokkupacok".

Fuzzy logika: Egy olyan eldöntés, ahol egy objektum típusából deduktálva nem csak igaz-hamis értékpár lehet, hanem van köztes érték is. Amike valami igaz is meg hamis is, vagy se nem igaz, se nem hamis.

Ennek értelmében itt lehet valami egyszerre A és A komplementere is, de legalább az egyiknek igaz kell, hogy legyen. A homokkupacnál viszont láttuk, hogy ez nem mindíg igaz vagy teljesül.
Ezt (az arisztotelészi logikát) Boole foglalta axiómarendszerben. Ehhez képest felmerültek a többértékű rendszerek. Példa: A háromértékű rendszer: Igaz-1 | Hamis-0 | Eldönthetetlen-0.5
Példa: Az értelmezésre, feltéve A és B független érték készletet:
ŁUKASIEWICZ: (alap logika)

A	B	És (Metszet)	Vagy (Unió)	Implikáció	Ekvivalencia	A negáltja
0	0	0	0	1	1	1
0	0.5	0	0.5	1	0.5	1
0	1	0	1	1	0	1
0.5	0	0	0.5	0.5	0.5	0.5
0.5	0.5	0.5	0.5	1	1	0.5
0.5	1	0.5	1	1	0.5	0.5
1	0	0	1	0	0	0
1	0.5	0.5	1	0.5	0.5	0
1	1	1	1	1	1	0

BOCHVAR: (nonsense értelmezés)

A	B	És (Metszet)	Vagy (Unió)	Implikáció	Ekvivalencia	A negáltja
0	0	0	0	1	1	1
0	0.5	0.5	0.5	0.5	0.5	1
0	1	0	1	1	0	1
0.5	0	0.5	0.5	0.5	0.5	0.5
0.5	0.5	0.5	0.5	0.5	0.5	0.5
0.5	1	0.5	0.5	0.5	0.5	0.5
1	0	0	1	0	0	0
1	0.5	0.5	0.5	0.5	0.5	0
1	1	1	1	1	1	0

KLEENE: (strong 3-valued logic)

A	B	És (Metszet)	Vagy (Unió)	Implikáció	Ekvivalencia	A negáltja
0	0	0	0	1	1	1
0	0.5	0	0.5	1	0.5	1
0	1	0	1	1	0	1
0.5	0	0	0.5	0.5	0.5	0.5
0.5	0.5	0.5	0.5	0.5	1	0.5
0.5	1	0.5	1	1	0.5	0.5
1	0	0	1	0	0	0
1	0.5	0.5	1	0.5	0.5	0
1	1	1	1	1	1	0

HEYTING: (intuicionista háromértékű)

A	B	És (Metszet)	Vagy (Unió)	Implikáció	Ekvivalencia	A negáltja
0	0	0	0	1	1	1
0	0.5	0	0.5	1	0	1
0	1	0	1	1	0	1
0.5	0	0	0.5	0	0	0
0.5	0.5	0.5	0.5	1	1	0
0.5	1	0.5	1	1	0.5	0
1	0	0	1	0	0	0.5
1	0.5	0.5	1	0.5	0.5	0
1	1	1	1	1	1	1

REICHENBACH: (háromértékű kvantumlogika)

A	B	És (Metszet)	Vagy (Unió)	Implikáció	Ekvivalencia	A negáltja
0	0	0	0	1	1	1
0	0.5	0	0.5	1	0.5	1
0	1	0	1	1	0	1
0.5	0	0	0.5	0.5	0.5	0.5
0.5	0.5	0.5	0.5	1	1	0.5
0.5	1	0.5	1	1	0.5	0.5
1	0	0	1	0	0	0
1	0.5	0.5	1	1	0.5	0
1	1	1	1	1	1	0

(VALAKI NÉZZE ÁT EZEKET PLIZ)
BOCHVAR-logika a kétértékű logika egyik alaptulajdonágát sem elégíti ki, ugyanis ez bármely műveletre eredményt 0.5 ad, ha valamelyik operandus értéke 05. (Hasonlóan a NaN értékhez)
Ez a 3 értékű logika általánosítható N értékre is. N értékű logika igazságterét (k/(N-1)) jelöli, ahol k=0,1,2,...N-1.

Implikáció: Ha A implikálja B-t, akkor ha A igaz akkor B-nek is igaznak kell lennie.

Igények és motivációk

A homokkupac paradoxont és ahhoz hasonló paradoxonokat feloldhatunk formális definíciókkal is de használhatunk fuzzy logikát.
Régóta igény van egy olyan rendszerre, ami ezeket a paradoxonokat fel tudja oldani emberi segítség nélkül. Ami fontosabb, az az, hogy ezeket a paradoxonokat autómatikusan fel lehessen oldani.
Ez is egy úgynevezett intelligencia.
Példák az ilyen gépekre:

• Kempelen Farkas (1734–1804): Sakkozó török
• Neumann János (1903–1957): Modern számítógép

(A modern számítógép magában nem sok intelligenciával rendelkezik)
Mesterséges Intelligencia: Egy olyan algoritmus, amely arra hivatott, hogy egy emberi viselkedést vagy egyéb termiszeti szabályszerű viselkedést tudjon utánozni minnél pontosabban. A legfőbb motiváció az volt, hogy ilyen szerkezeteket könnyen lehessen tervezni, vagy könnyen lehessen olyan módszereket találni, melyeket követve ilyen szerkezethez juthatnak az emberek. Példa: Önvezető autó.
De sajnos egy önvezető autó akár jövőbeli létrejöttét nem tudjuk se cáfolni, se bizonyítani, mivel biológiai viselkedést kell mimikáznia (ember vezetését).

Az is felmerül, hogy egyáltalán jó döntéseket hoz-e az autó, és azt mi meg tudjuk-e itélni. Példa:

• Az utas vagy a gyalogos élete a fontosabb?
• A fiatal vagy idős emberé a fontosabb? (Ha az ütközés valamelyikkel elkerülhetetlen)

Az is nehezíti a rendszert, hogy felülről nem korlátos információ egységgel kell dolgoznia egy ilyen programnak.
Megoldás: Közeli optimum keresésa a szimulációban. Erre lesz jó a fuzzy logika.

Fuzzy logika és közelítés

Összefoglalva a fuzzy halmazok és fuzzy logika megalkotásában a legdöntőbb motiváló erő kétség kívül a nagybonyolultságú műszaki feladatok megoldásának igénye volt.
Az 1950-es évektől kezdve a mesterséges intelligencia kutatás a Boole-logikát használta, mint formalitás. Ez azért jó, mert egyszerű a ha-akkor típusú implikációkat leírni a következtetési szabályokat. Implikáció: Adott A és B esemény. Ha A implikálja B-t akkor ha A igaz akkor B-nek is igaznak kell lennie. A Boole algebrában a legkönnyebben az (NOT A OR B)-vel lehet kifejezni. Fontosabb szabályok rá:
Modus ponens:
A IMPLIES B akkor következtetés: B igaz


Modus tollens:
A IMPLIES B akkor következtetés: ha NOTA igaz akkor NOTB is igaz


Hipotetikus szillogizmus:
A IMPLIES B és B IMPLIES C akkor következtetés: A IMPLIES C


Hát ez így magába nem sokat mond, de egy példa segítene szerintem. Példa: Tudjuk, hogy ha valaki tanár, akkor tanít.
Tudjuk azt is, hogy Tomi tanár.

Ebből azt a követekeztetést tudjuk levonni, hogy Tomi tanít, mert ő tanár és a tanárok tanítanak.
Függvényimplikáció: legyen x és y változó és A(x) és B(y) pedig valamilyen függvény, ami x és y függvényében szimbólikus igazságértéket vesz fel. Ekkor A(x) IMPLIES B(y) értelmes, és annyit jelent, hogy ha x értéke K (valamennyi konstans skalár) akkor az implikál valami y értéket. Szimbólikus igazságérték: Egy olyan Boole érték, amely azt jelzi egy A függvényre, hogy a kapott x változóra igaz vagy hamis értéket ad vissza. Ekkor már komplexebb dolgok is leírhatóak. Pl: jelölje X azt, hogy hány Celziusz fok van és legyen egy olyan függvény, ami megmondja, hogy fagy-e (mondjuk 0 fok alatt igazat ad, amúgy hamisat). Illetve van egy másik szabályunk: ha fagy, akkor havazik.
Ekkor meg tudjuk mondani, hogy ha -20 fok van, akkor fagy és akkor havazik is, mivel formális implikáció állítja ezt a tényt.

Ez így nagyon jónak tűnik viszont van egy kis probléma. Egy elég nagy probléma, ez az, hogy a paraméterek és szabályok növekedésével a megállapítás komplexitás exponenciálisan nő a mostani számítógépekkel.
Tétel: Ha a bemenet k változót tartalmaz melyek x1,x2...xk és ezeknek legyen T a deduktív korlátja, ekkor a szabályhalmaz felső korlátja T^k.

Bizonyítás: Minél finomabb a közelítés, annál nagyobb T, és 2-szer finomabb felosztás esetén nem 2-szer annyi-ra nő a szabályhalmaz, hanem 2^k-ra, mert az osztás = 2x több kombináció.
Deduktív korlát: Vegyünk X1,X2...Xn n darab fuzzy input változót. Ekkor T korlát jelöli a különböző logikai szimbólumok számának felső korlátját, amelyek ezek változókból és implikációjából konstruktálható. Itt már el tudunk képzelni egy AI macskát, aminek az a lényege, hogy attól függően, hogy hol az egér, menjen oda. A macska fejében egy olyan szimbolikus szabálybázis van, mely az egér pozícióját, mozgási jellemzőit és minden egyéb szükséges információt figyelembevéve következtet arra, hogy a következő mintavételi pillanatban hol lesz az egér. A macska az egér mozgásterét úgy látja, mint egy raszterháló által felosztott síkidomot. A következtetés eredménye a raszterháló egy mezeje; ezen belül a macska a kimerítő keresés módszerével határozza meg az egér tényleges helyzetét. Ha a macska fejében finom modell van, azaz nagyszámú szabály, akkor a következtetés eredménye egy kis méretű rasztermező lesz, és ezért a mező azonosítása után a macska hamar meg fogja találni az egeret. A probléma ilyenkor onnan adódik, hogy a macska fejében lévő finom modell nagy szabályszámot feltételez, és ezért a macska következtetési ideje megnő (ez persze visszahat arra is, hogy az egér pillanatnyi helyzete mégiscsak kisebb pontosággal adható meg, hiszen hosszabb idő alatt az egér nagyobb távolságot mozdulhat el). Ha ezzel szemben olyan megoldást választunk, ahol a macska következtetési ideje rövid, ez kis szabályszámot, következtetésképpen pontatlan modellt jelent, vagyis a macska hamar kikövetkezteti az egér új helyzetét jelentő rasztermezőt, de ez a rasztermező nagy kiterjedésű lesz, és ezért a keresés második fázisa lesz hosszadalmas. [LSZ Jegyzet]
Vajon létezik-e optimális kompromisszum? Hát, lehet, de nem triviális. Bebizonyítható, hogyha a robot gondolkodási ideje és a mezőn belüli keresés lépésszáma rögzített költségértékeket jelentenek, akkor a szabálybázis méretének optimuma számos konkrét már meghatározott modellfajta esetén egyértelműen meghatározható.
Bizonyítás: 2 input változóra, a és b-re. (Amennyiben ezeknek a szabályai ekvidisztánsan helyezkednek el és legfeljebb 2 szabály tüzel egyszerre.
Ekkor T1 = c0*r+c1 ahol r a szabályok száma és c0 és c1 alkalmaz konstansok.
A keresési idő: T2 = 2*c2/(r-1) ( arányos a konzekvens halmazok tartójának hosszával, ami nyilván fordítottan arányos a szabályok számával)
Ahol c2 a rasztermező keresési költségének tényezője.
Az összesített T ekkor T = T1+T2 = c0*r + c1 + 2*c2/(r-1). Ez kiterjeszthető szabályszámra vonatkozó optimumra deriválással tetszőleges R mennyiségú szabályra.
Hát ez így még nem annyira érthető, de később lesznek rá példák.
(Még bővítem, ha lesz időm) (10.oldal)

Illesztések

Ezekből nagyon sok lesz.

Természetes illesztés: 2 operandusos művelet. legyen L schéma aminek attribútumai a1,a2,...an meg egy M schéma aminek b1,b2,...bn. Feltételezzük, hogy az attribútumok közott vannak páronként azonos nevűek. Az A[i1] azonos B[j1]. Ilyen párból legyen K db. egy A[ik] azonos nevű B[jK]. Annak a 2 relációnak a természetes illesztését. Példa: Ha R és S egy reláció akkor R ⨝ S jelölje R és S természetes illesztését.

Példa: Szelekcióra: Dolgozók tábla:

Név	Életkor	Munkahely név
Feri	23	KFC
Jani	44	Rheinmetall
Juli	33	KFC

Munkahelyek:

Munkahely név	Ki vezeti?
KFC	Péter
Rheinmetall	Jani

Dolgozók ⨝ Munkahelyek illesztés eredménye:

Név	Életkor	Munkahely név	Ki vezeti?
Feri	23	KFC	Péter
Jani	44	Rheinmetall	Jani
Juli	33	KFC	Péter

Itt a Munkahely név alapján csatoltuk össze a 2 táblát. Fontos, hogy a vetítés és kiválasztásnál R schémát és halmazt is lehet megadni, vagy csak simán oszlopneveket.

ER modellezés gyakorlati anyag

Refresher:

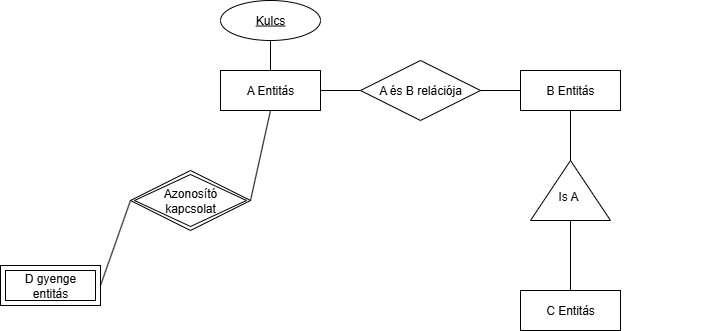Ezen az ábrán rajta van kb. minden amit eddig az ER modellekről tanultunk.
Egy pár érdekes kérdés erről az ábráról:

1. Mi a különbség az ábrán (működésben) az "Is A" és a determináló kapcsolat + gyenge egyed kapcsolat között? Megoldás: az "Is A" C egyed megörökli/átveszi a B egyed kulcsait, míg a determiáló kapcsolat + gyenge egyednél a gyenge egyed az A egyed kulcsával kap egyediséget. Nem örökli meg se nem veszi át, csak azzal együtt egyediséget kap. De leképezésbe mind a kettőt lehet használni, majdnem ugyanazok. Fontos lesz majd, hogy lássuk, hogy mikor melyiket érdemes inkább.
2. ER modellbe az idegen kulcs nincs jelölve.

Filmtár feladat

Példa: Szeretnénk egy film tároló adatbázit modellezni ezen kritériumok alapján:

• 1 Filmet több ember tud írni.
• 1 Filmbe lehet több rendező vagy színész.
• A filmnek van Címe, ami egyedileg azonosítja (ebből kiderül, hogy ez a kulcs), hossza percben, megjelenés dátum, kor besorolás, bevétel.
• Minden embernek kell van egy: Neve; lakcíme; személyi száma, ami egyedileg azonosítja és telefonszáma.

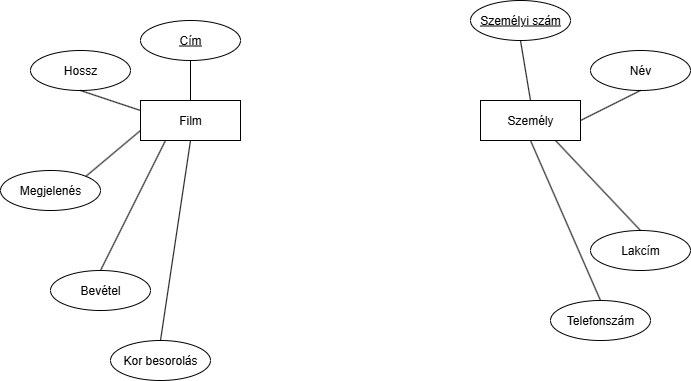Kezdjünk el ötletelni ez alapján. Csinálhatunk egy Személy egyedet, amibe benne van az összes típusú ember attribútuma és egy Film egyedet: No, hogyan tovább? Kéne nekünk jelezni, hogy vannak írók, rendezők és szereplők. Próbálkozzunk az "Is A" kapcsolattal: 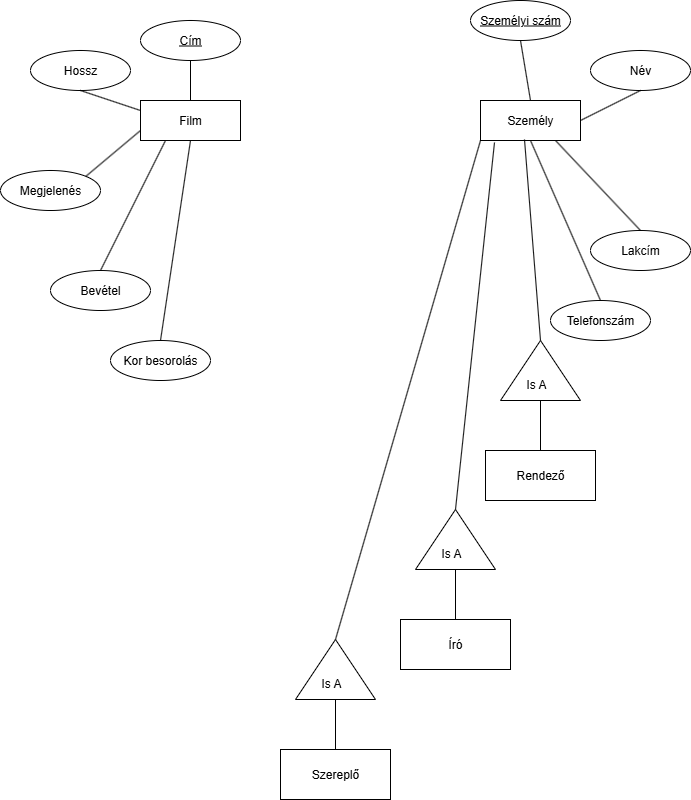Valahogy az a tervünk, hogy a leszármozott egyedekből csinálunk kapcsolatokat. Nos, ez nem annyira jó, mert mi van, ha valaki egyszerre szereplő és író is? Akkor redundás lesz a modell.
Hát, akkor új ötlet kell:
Megoldás: a szerepköröket kapcsolatként vesszük fel: 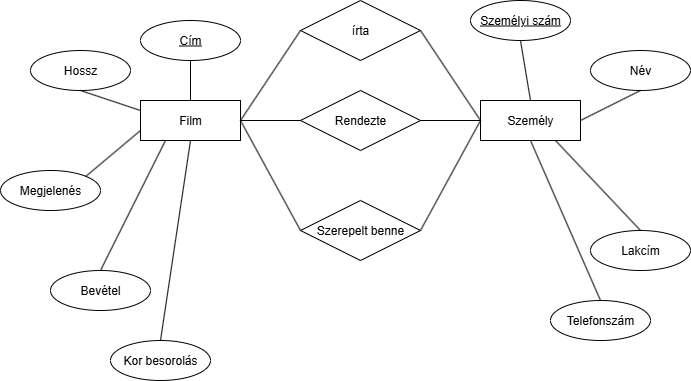Nos, így már egyértelmű minden: 1 ember tud lenni egyszerre töb körben is és több filmben is tud lenni. Viszont itt egy újabb bökkenőben ütközünk:
Mi van akkor, ha valaki 2 iker szereplőt játszik 1 filmben (pl: Axel és Alex)?
Próbálkozhatunk úgy, hogy felveszünk egy mezőt a "Szerepel ebben" relációhoz: 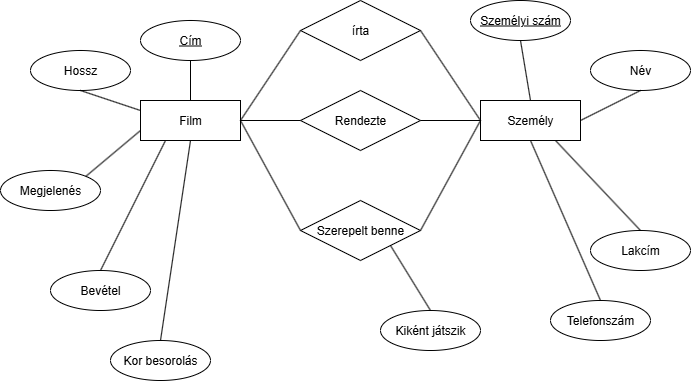Nos, ez majdnem szép és jó de 1 nagyon fontos dolgot meg kell jegyezni:
A reláció a tulajdonságai alapján nem képes egyedet azonosítani. Lehet több Axel is több filmben és akkor már nem működik ez.
Akkor próbáljuk azt, hogy felveszünk egy Szerep egyedet ahol a név lesz az kulcs és egy ternáris relációt csinálunk: 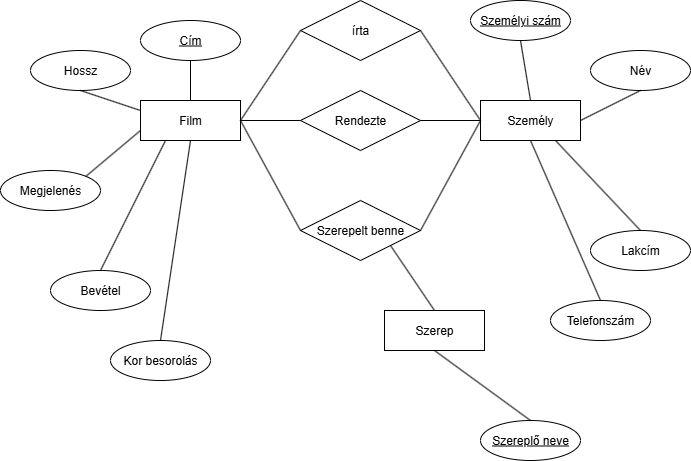Ez már jobb, csak az a baj, hogy a szereplő neve még mindíg nem azonosítja egyedileg a szereplőt. Példa: Van több Batman film és több Batman is azokban amit több ember is játszik. Nem csak 1 ember játsza az összes Batman-t.
Ötlet: Gyenge egyeddé tesszük a Szerepel egyedet és a Film által lesz neki egyedisége. Pl: Melyik filmbe Batman?: 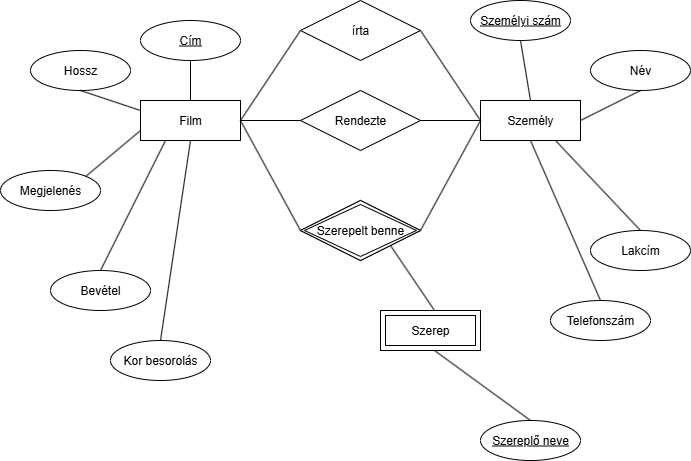Hát ez szép, mostmár minden egyértelmű. Vagy mégsem? Most az a baj, hogy az ER modell nem mondja meg, hogy hogyan kell értelmezni ezt a ternáris determináló kapcsolatot. Hogyan is kéne ezt? Emlékezzünk: Nem szabad ternáris kapcsolatnak csak 2 kötését használni, és a harmadikat kihagyni. Igazából már megvan, mire gondolunk és az jó is csak azt tisztázni kell. Ennél mi sem egyszerűbb, bontsuk szét a ternáris kapcsolatot 2 bináris relációra és akkor tudunk csak 2 egyedet relációt használni és értelmezni: 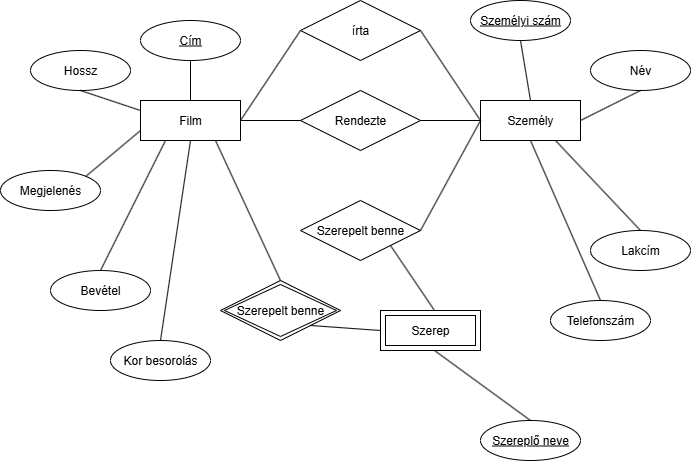Ezzel az 1. feladatot el is végeztük. Fontos leírni, hogy mikor mire gondoltunk, mert egy ER modellnek igazán csak indoklással van értelme.
A felső vezetés meg van elégedve a modellel, de egy újabb feladatunk van:

• Csináljunk olyan film egyedeket, aminek vannak extra mezői.
• Legyen egy Krimi film, amiben vannak még külön áldozat és gyilkos szereplők is.
• Legyen egy természetfilm, ami bizonyos helyeken volt forgatva bizonyos országokban.

Ennél már jusztifikáltabb az "Is A" leszármozó kapcsolatot használni, mert tudtommal nincs olyan film, ami természetfilm és krimi is egyszerre:
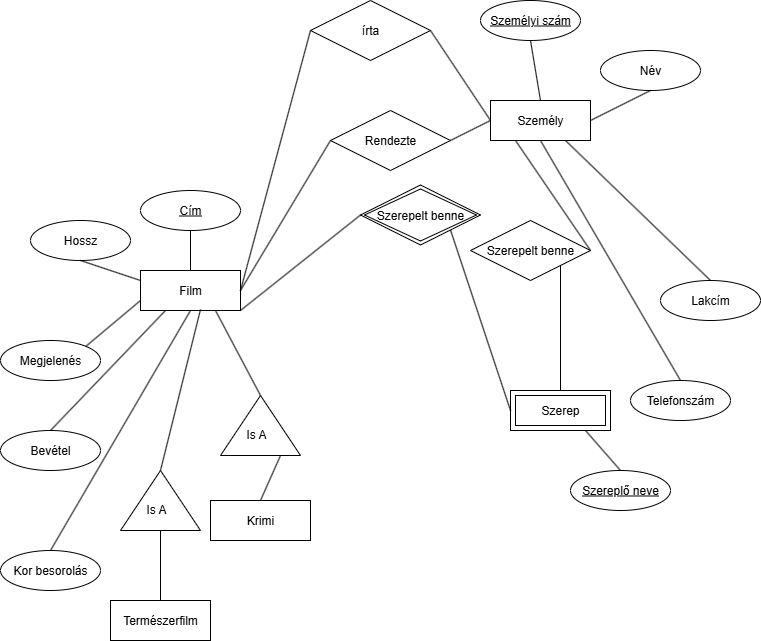Hogy legyenek a természetfilmnél a helyek? 1 hely 1 országban lehet csak, csinálhatunk kapcsolatot is, de csinálhatunk egy Hely egyedet aminek van egy ország mezője:

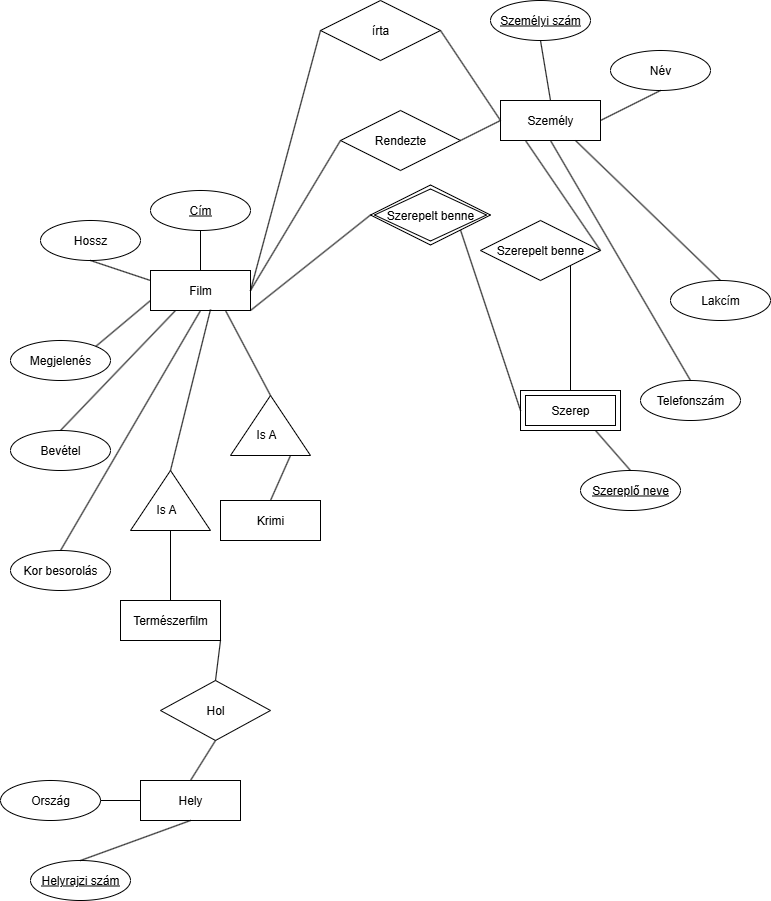
A helynél használhattunk volna hely ID-t vagy hely azonosítót, de az általába "csalás". Jobb valami megfoghatót adni kulcsnak.

Milyen ötlet van a krimire? Csinálhatunk 2 egy-többhoz kapcsolatot a Szerepből, ami azért egy a többhöz, mert már film specifikusra van szűrve a szerep a determináló kapcsolat miatt: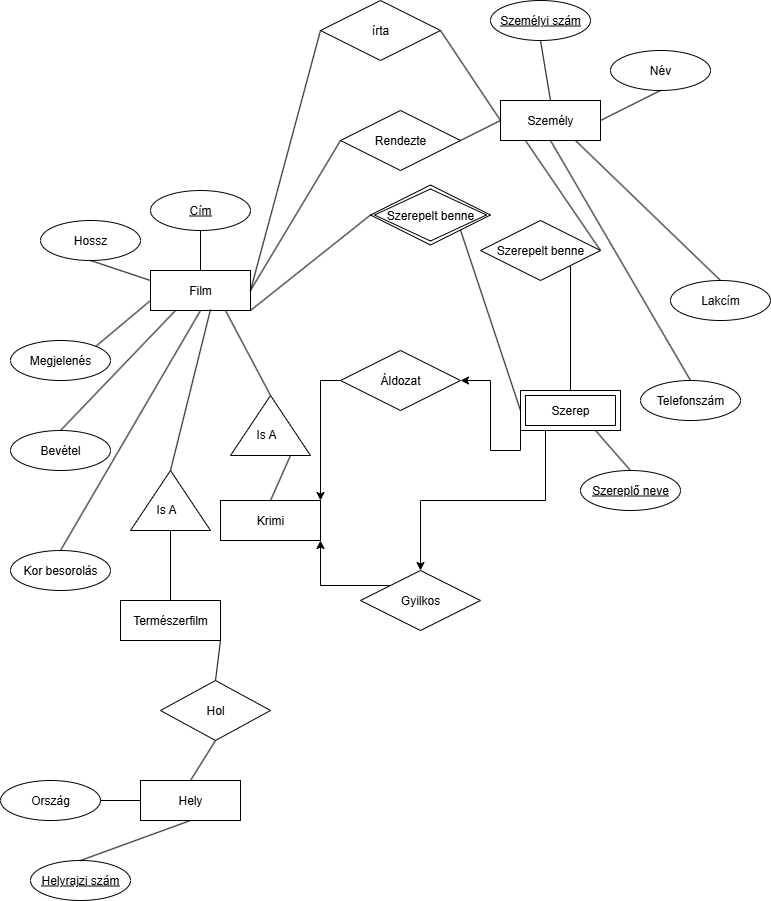 Ezzel ez a feladat kész is volna.
Jó tipp: Ha a feladat számos relációt akar, Pl: 10 tanár tanít 1 osztályt, akkor nem kell kirajzolni a 10 darab t1,t2...t10 relációt, elég odaírni, hogy: Ezt nem lehet szépen lemodellezni de még tudjuk, hogy 10 tanár tanítja azt az osztályt.

Iskola feladatra visszatérünk

Legyen egy iskola modellünk, ahol modellezzük, hogy vannak iskolai osztályok és személyek is:

• Az iskolának van neve és helyrajzi címe. A neve egyedileg azonosítja.
• Legyen egy tanár, aminek van egy neve és lakcíme, születési dátuma, valamint tanár tud igazgató lenni. Tanár lehet osztályfőnök is.
• Legyen egy diák, aminek van egy neve és lakcíme, születési dátuma.
• Legyen egy osztály egyed, aminek van egy neve (mondjuk 12.A) és létszáma.

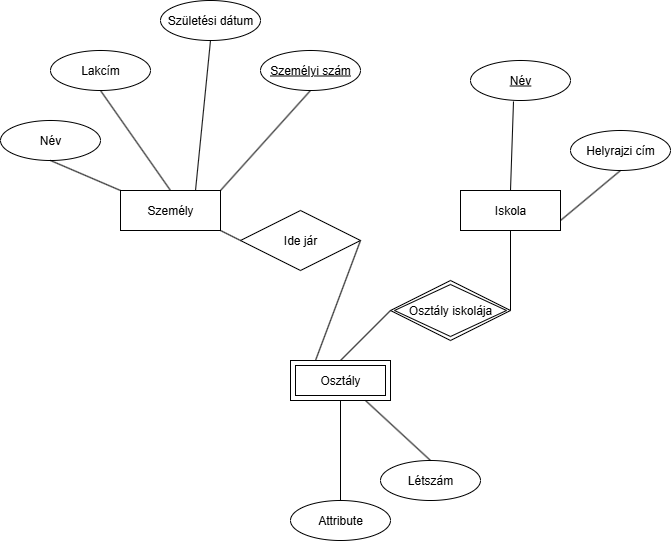Példa: Egy lehetséges implementáció így nézhet ki: Megjegyzések: Ebből az ábrából hiányzik a tanár osztály valamint, ha az ember megfigyeli, az osztály létszáma mező kicsit redundáns, mert azt ki tudjuk számolni abból, hogy milyen diákok kapcsolódnak az osztály egyedhez. (És abból mennyi).
Ha feltételezzük, hogy diák nem lehet tanár, akkor példáúl az "Is A" kapcsolattal létrehozhatunk egy tanár egyedet: 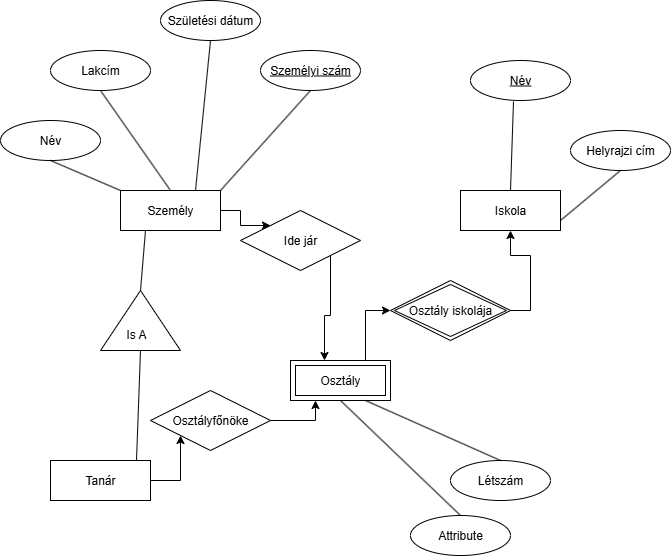Jelezzük, hogy egy tanár lehessen igazgató: 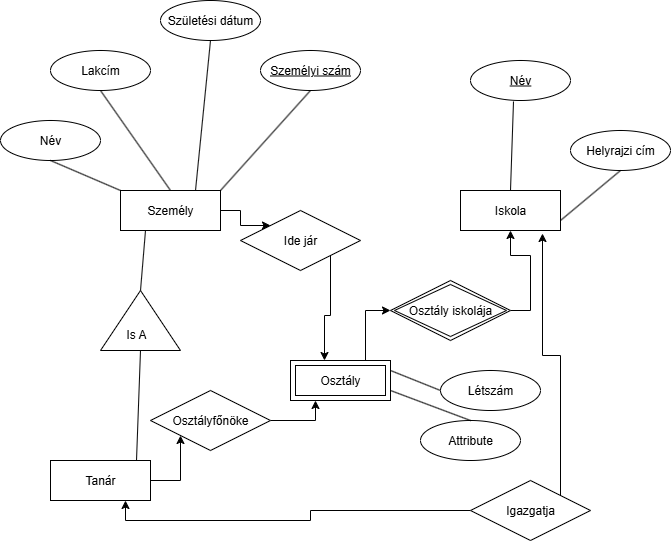1 ember csak 1 iskolát tud igazgatni (törvény szerint 2025-ben, Magyarországon) és egy iskolának csak 1 igazgatót engedünk. Jelezzük, hogy egy tanár taníthasson tárgyakat és osztályokat is: 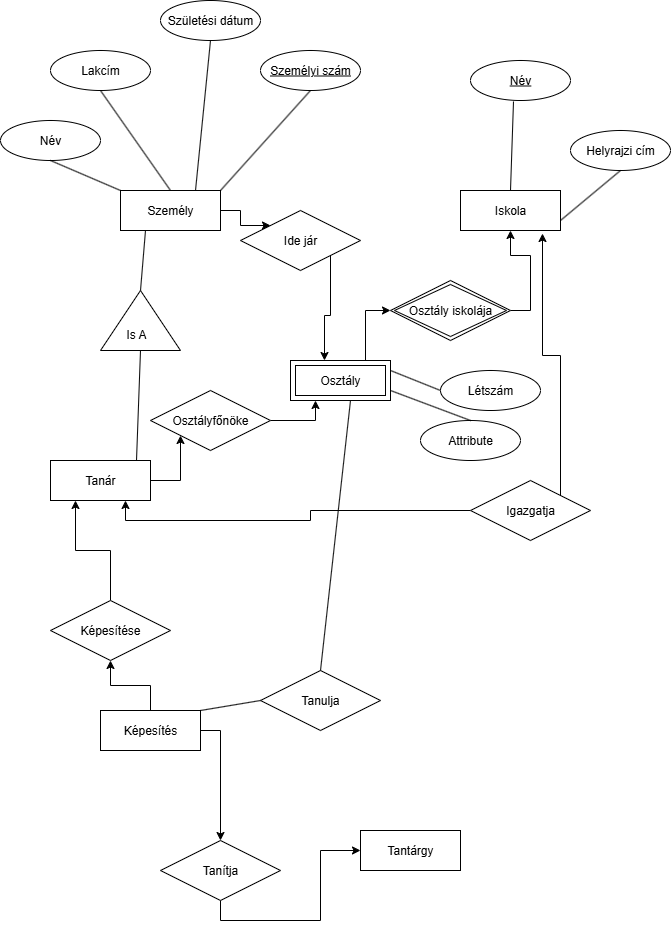Magyarázat: 1 tanárnak lehet több képesítése, és egy képesítéshez tartozhat több tárgy. Pl: Informatika tanár képesítéshez tartozhat a programozás alapjai 1, 2 és 3 is.
Az osztályok tanulhatnak több tárgyat több tanártól is. Pl: lehet 2 programozás alapjai 1 tanár is.
Miért nem jó, ha a képesítés egy trinary reláció lenne? Azért, mert akkor 1 csoport nem tanulhatna 1 tárgyat több tanártól? Pl: Nem lehetne a 12.A csoportnak kettő programozás alapjai 1 tanára.

Relációs adatmodell part 2: Származtatott műveletek

Főbb megfogható leírás: Adatokat egymáshoz való viszonyhoz való rendelése. Pl: Táblázat sor vagy kapcsolat is.
Példa: Az adatok kapcsolására:

• Pointereken keresztül navigálni, imperatív módon, ide-oda. Végeredmény összeszedése.
• Összetartozó adatok egymásmellé helyezése. Ugyanabban a rekordban => Össze vannak rendelve, van kapcsolat adatok között.
• Az összekapcsolandó értékek mellé rendelünk idegen kulcsokat, és kulcs-idegen kulcs azonossága mutatja a relációt.

Ezek fogják meghatározni, hogy egy adatbázis kezelő rendszer milyen hatékony lesz, milyen utasításokat fog támogatni.
Manapság ezeknek a módszereknek a kombinációját láthatjuk sok formában. Pl: NoSQL az első példára.
Példa: unóra:

A
alma
körte
narancs

B
barack
körte
cseresznye

A UNION B
alma
körte
narancs
barack
cseresznye

Példa: különbség képzésre:

A
alma
körte
narancs

B
barack
körte
cseresznye

A \ B
alma
narancs

Példa: hányados képzésre:
A hányados akkor hasznos, ha a következő diákok közül ki szeretnénk választani, hogy kik azok a tanulók, akik minden S-ben szereplő tantárgyat tanulnak?

Tanuló	Tantárgy
Anna	Matek
Anna	Történelem
Béla	Matek
Béla	Történelem
Béla	Fizika
Csilla	Matek

Tantárgy
Matek
Történelem

E ÷ S
Anna
Béla

Fontos új, magasabb szintű műveleti szekvenciák használata, megjegyzése. Példa: Természetes illesztés: Ennek eredménye: Descartes szorzat->Szelekció->Projekció.
Eddíg a műveleteink véges relációkból véges relációkba képeztek, ezért zártak. Sosem lesz végtelen halmaz a lekérdezés végeredménye.
Példa: Természetes illesztésre:
2 olyan reláció, ahol A és B táblának, a,a,b, valamint b,c,b és S(s) Séma: A|C : a,b és c,c.

A
a
a
b

B
b
c
b

Sémák:

A	C
a	c
b	c

Első lépésben Descartes szorzat:

R.A	R.B	S.A	S.C
a	b	a	c
a	b	b	c
a	c	a	c
a	c	b	c
b	b	a	c
b	b	b	c

Most a szelekcióval válogassunk a sorok közül. A Séma marad 4 soros:
σR.A=S.A (r x s)
1. sorban a=a, igaz, másodikban a!=b, így tovább:

R.A	R.B	S.A	S.C
a	b	a	c
a	c	a	c
b	b	b	c

Ezután keletkezett 2 oszlop, a természetes illesztés attribútuma miatt amik feleslegesek. (Ezek azonosították a 2 különböző táblát).
A sorok sorrendje, mivel halmazelemek közömbös.
R⋈S:

R.A	R.B	S.C
a	b	c
a	c	c
b	b	c

Az S.A sor redundáns volt.
Miért fontos ez? Ez arra jó, ha 2 táblát közös azonos értékek alapján össze akarjuk kapcsolni.
Példa: Dolgozókat össze akarunk kapcsolni hogy hol dolgoznak.
Az előző példába az R kódok és S elnevezésekből olyan dolgozói névlistát, ahol az adott kódú osztályhoz megmondható, hogy ki dolgozik ott, vagy, hogy mi az osztály neve.
Az eredmény olyan lesz, hogy tartalmazni fogja az osztály nevét, a dolgozókat és az osztály bővebb neve.
A természetes illesztést lehet általánosítani: Theta Join.

Theta illesztés: 2 halmaz descartes szorzata, és utána egy olyan szelekció, ahol megköveteljük, hogy az 1. sémában i. oszlopa értéke THETA viszonyban legyen az S j. oszlopának értékével. Ez a sima SQL JOIN-nak felel meg.

Ennyi volt a származtatott művelet.
Fontos, hogy a Származtatott műveletek nem bővítik azt, amit az alapműveletekkel el lehet érni.

A Relációalgebra alkalmazása

Legyen egy adatbázis aminek a 4 következő reláció sémája: A séma:

• AK
• AN
• AE

Bl séma:

• D
• O

M séma:

• D
• AK
• DB

BZ séma:

• O
• B

Ezek formalizmusok, nem kell, hogy értelme legyen. Az AK, D és O kulcs.
Pl: Kérdezzük le, hogy a B értékeihez milyen attribútumok tartoznak, ahol a D értéke X.
Lekérdezhető, nem tudjuk igazán micsodát, mert nem adtunk rendes nevet de formálisan le lehet kérdezni.
A D és B értékek nem tartoznak össze direktbe, de van egy O attribútum ami azonos értékei mentén össze lehet őket THETA joinolni.
SELECTION D>2017.03.23. b(Bl) NATURAL JOIN bz(BZ)
Magyarázat: b-hez Bl séma tartozik, bz-hez pedig BZ sémát. Ez a lekérdezés helyes.
Az ilyen módon az adatokból kinyert adatokhoz próbáljunk meg tudást hozzárendelni.
Pontosíthatnánk, hogy a D,AK... attribútum mit jelent.
Új példa:
Áru reláció:

• [P]Árukód
• Árunév
• Ár

Bevétel reláció:

• [P]Dátum
• Összeg

Mennyiség tábla:

• [P]Dátum
• Árukód
• Darab

Befizetés tábla:

• [P]Összeg
• Bef

Pl: A Befizetés értéke 4000 FT, ennyit hagynak a kasszába visszajáróhoz.
2017. 09. 23. utáni napok esetén mi volt a bankba befizetett érték?
A formalizmust már emberi nyelven is meg lehet fogalmazni.
A megoldás egy 2 oszlopű táblázat lesz, X napon Y FT-ot fizettünk a bankba.
SELECTION Dátum>2017.09.23. Bevétel(BEVETEL) NATURAL JOIN Befizetés(BEFIZ)
De hogyan kéne megszülni ezt a lekérdezést? Ahol nem triviális a szemantika, ott egy leírást adnak általába gyakorlati rendszerekben.
Pl: A telekomnál tartozik cím1,cím2,cím3,cím4,cím5. És ott le van írva, hogy a cím1 a szerződés kötő címe, a 2. a felhasználó lakcíme, a 3. az ... címe.
Nem triviális, hova küldjük a fizetési felszólítást? Melyik címre? Pl: Az Oracle adatszótárában (Data dictionary) ezek az értelmezések benne vannak.
Visszatérve, előszőr ki kell hallani, hogy mi adja az eredményhalmaz elemeit. Ehhez képest mik azok az egyéb feltételek, amik az eredményhalmaz értékeit befolyásolják.
A példa kedvéért formálisan felírva mégegyszer:
B lekérdezés definícója az, hogy 2017 szept 23. utáni napok bevételei:
BEVÉTEL NATURAL JOIN BEFIZ -> Ennek a sémákra semmi értelme nincs, nincs adat amit Descartes szorozni meg kiválasztani lehetne.
Szigorú formalizmus szerint hülyeség, de belátható, hogy ez 2 reláció:
SELECTION Dátum>2017.09.23. (BEVÉTEL NATURAL JOIN BEFIZ).
Ennek eredménye egy olyan reláció lesz, aminek az 1. oszlopában a Dátum lesz (3. oszlopban Descartes szorzat miatt megjelenik megint, de azt kivehetjük), a 2.-ban pedig a bezifezések. Vetítéssel végül D és B-re szűrni:
PROJECTION Dátum,Bef SELECTION Dátum>2017.09.23. (BEVÉTEL NATURAL JOIN BEFIZ).
Fontos, a napi bevétel lehet azonos 2 napon, de a reláció logikájában 2-szer ez az összeg ugyanúgy nem fog megjelenni. Egszer bele van írva, semmi probléma.
Mi van, ha 2 operandus relációban több attribútum neve azonos? Semmi, mert az összes azonos nevű attribútumnak páronként azonosnak kell lennie definició szerint.
Fontos: Szelektálni mindent lehet, de majd később írok példákot, hogy hol és mi optimális.
Legyen F-el egy lekérdezés, ahol: Egy A1 kódú árú neve, és hogy mennyit adtak el 2025.09.08.?
Megoldás:
PROJECTION Árunév,Eladott DB SELECTION Dátum>2025.09.8. (...). Ennyit alapból kiszűrhetünk. Már csak azt kell megmonadni, hogy hogyan kell ezeket kiszedni 1 sorban.
Ezt az árú táblából lehet kiolvasni, az árúkód mennyiség táblával való illesztése:
PROJECTION Árunév,Eladott DB száma SELECTION Dátum>2025.09.8. AND Árukód=A1 (Áru NATURAL JOIN Mennyiség)
Relációalgebra segítségével mindenféle lekérdezést meg lehet csinálni.

Lekérdezések

Lekérdezésekkel imperatívan eddíg le tudtunk mindenfélét kérdezni.
Itt nem csak azt kell megadni, hogy mit akarunk tudni, hanem, hogy hogyan kell azokat az adatokat elérni. Ez macera lehet.
Megoldás: Deklaratív lekérdezési módot csinálunk, nem kell megmondani, hogyan jussunk el az eredményhez, csak jellemezzük az eredményhalmazt.

1. Labor összefoglaló

Az Oracle adatbáziskezelő története

Ezt az eszközt a CIA kezdte el fejleszteni 1970-ben. (Helyesebben, az ő megbízásukkal)
Nevét a kinyilatkoztatás, prófécia szavakból kapta.

Az Oracle felépítése

Az Oracle egy objektum-relációs adatbáziskezelő:

• Alapvetően kliens-szerver felépítésű
• Oprendszertől függően lehetővé teszi a többtaszkos, több felhasználós működést, és az adatok egyidejűleg való felhasználását.
• Térben elosztott rendszerként is képes működni.
• A fontosabb hálózati protokollokkal és rendszerprogramokkal is képes együtt működni.
• Támogatja a szoftverfejlesztés minden egyes szakaszát.
• Képes együttműködni ez egyes fordítókkal és IDE-kkel.
• Tetszőleges adatmennyiséget képes kezelni (variáló hatékonysággal)
• Napi 24 órás rendelkezésreállást biztosít.
• Magas szinten képes biztosítani az adatok integritását.
• Alkalmas összetett struktúrák tárolására. Pl: Objektumok, multimégia adatok, eljárások.
• Az Oracle, mint cég aktívan támogatja a rendszert.
• Fejlett rendszerfelügyelet biztosítható az Oracle Management Server és a hozzá kapcsolódó Agentek segítségével. Ekkor az Enterprise Manager alkalmazás segítségével egy tetszőleges méretű adatbázis-park adminisztrálása/távfelügyelete válik lehetővé.

A szerver alatt minden esetben egy adatbázist értünk. Az adatbázisban tárolódnak a Felhasználói és rendszeradatok míg a szerverpéldány a szolgáltatás futtatásához szükséges folyamatok és threadek összessége.
Egy számítógépen lehet több adatbázis is. A legmagasabb színtű névvel ellátott tárolási egység az adatbázis.

Logikai felépítés

Az adatbázisokat tablespacekre, vagy táblahelyekre oszthatjuk, ez a legnagyobb logikai tárolási egység.

• system: Ide jönnek a rendszer információi. Pl: Adatszótár
• sysaux: A kiegészítő táblahely a system mellett. 10g verzióban jelent meg. Ide került az adatbázis néhány olyan funkcionalítása, mint a LogMiner vagy Data Mining csomag.
• rbs: Az adatbázison végzett műveletek naplója.
• temp: Átmeneti csomagoknak van fenntartva.
• tools: Más alkalmazások által használt minta tárhely.
• users: Az általános Felhasználói mintatárhely.

Database link: olyan szinonima, amelyen keresztül nem objektumokat, hanem adatbázisokat érhetünk el. Említettük, hogy egy szerverszámítógép több adatbázist is tartalmazhat, sőt lehetnek akár elosztott, azaz több, különböző számítógépen tárolt, azonban adatait tekintve összefüggő adatbázisok is. Ilyen esetekben szükségünk lehet kapcsolódási pontok definiálására. Data dictionary: csak olvasható táblák és nézetek gyűjteménye, amelyek a rendszer mindenkori állapotát rögzítik. Ennek megfelelően megtalálható benne, hogy milyen felhasználók vannak a rendszerben, azok mely objektumokhoz férhetnek hozzá; milyen kényszereket kell érvényesíteni az egyes mezőkre; milyen alapértékek vannak beállítva az egyes oszlopokra; mennyi helyet foglalnak az egyes objektumok, mennyi hely van még szabadon; ki, mikor lépett be az adatbázisba és mit módosított vagy nézett meg stb. Cluster: Azonos kezelési vagy hozzáférési módot igénylő adatok egyetlen csoportos, fizikai helye.

Adattípusokról röviden

• CHAR(n): Egy n méretű string, ha nagyobb stringet akar valaki belerakni, mint n, akkor levágja az n+1 és utána lévő karaktereket. Ha kevesebbet, akkor szóközökkel kitölti a maradék helyet. Ha n nincs specifikálva akkor n=1-et használ.
• VARCHAR2(n): Változó hosszúságó+ú sztringet tud tárolni, olyan mint a char, csak kisebb inputnál nem tölti ki a maradék helyet.
• NCHAR(n),NVARCHAR2(n): A CHAR és VARCHAR unicode változata.
• CLOB: Nagyméretű szövegek tárolására alkalmas típus. Amennyiben fentieknél nagyobb méretben szeretnénk karakterfüzért tárolni (nem kell megadni felső korlátot), akkor érdemes a megfelelő mezőt CLOB-nak (Character type Large OBject) definiálni. A CLOB-nak is van maximális mérete, de ez kellően nagy: elméletileg 4 gibiblokk is lehet.
• Number(p,s): Egy számot tároló adattípus, a p a szám összes jegyének száma, az s pedig az, hogy a tört vessző mögött mennyi jegy legyen p-ből.
• DATE: Dátum tárolására alkalmas adattípus. Az Oracle valamennyi olyan dátumot képes tárolni, amely i.e. 4713. január 1. és i.sz. 9999. december 31. közé esik. Hét mezőből áll: század, év, hónap, nap, óra, perc, másodperc. Sok szármoztatott adattípusa van.
• ROWID: Az adatrekordok egyedi logikai és fizikai azonosítója. Minden tábla rendelkezok ROWID segédoszloppal
• UROWID: Az UROWID típus olyan rekordok logikai egyedi azonosítóját tárolja, amelyek fizikai helye más rekordokon végzett műveletektől, vagy az Oracle adatbázis-kezelő hatáskörén kívül eső körülményektől függ. Az ilyen rekordokat tartalmazó táblákban a ROWID nevű segédoszlop UROWID típusú. Az ún. index-szervezésű táblákban (Index-organized Table, IOT) a rekordok az indexek levelében tárolódnak, amelyek új rekordok beszúrásakor/törlésekor, meglevők módosításakor áthelyezésre kerülhetnek más fizikai blokkba. Az index-szervezésű táblák rekordjainak UROWID típusú azonosítója mindaddig változatlan marad, amíg az elsődleges kulcs értéke változatlan. Az Oracle adatbázison kívül tárolt táblák rekordjainak azonosítói szintén UROWID típusúak

Szinonima (Synonim): egy táblára, nézetre vagy számlálóra több név is megadható a szinonimák segítségével. Lehetőségünk van tehát rövidíteni vagy átlátszóvá tenni az egyes objektumok tárolási helyét. Van nyilvános (public) és rejtett (private) szinonima is. A nyilvános szinonima mindenki számára hozzáférhető, míg a rejtett szinonima csak a felhasználók egy meghatározott körének érhető el. A nyilvános szinonima létrehozása és eldobása speciális jogokhoz köthető.

Index (Index): adatokhoz való hozzáférést (általában) gyorsító eszköz – az Oracle-ben alapesetben egy B* fa.

Fizikai felépítés

Egy datafile-ban több table is lehet, és egy table több datefile-ban is lehet egyszerre.
Fizikai felépítés: Segment->Extent->Data block.
Rollback szegmens (rollback segment): minden megváltoztatott, de még nem committált érték, elem adatát tárolhatjuk itt. Az újabb Oracle verziókban (9-től felfelé) ez a szegmens nem létezik.
Adatszegmens (data segment): minden táblában megtalálható adat egy ilyenben foglal helyet. Indexszegmens (index segment): a különféle indexek hatékony tárolására alkalmas szegmens. Ideiglenes szegmens (temporary segment): minden művelet végrehajtásához az Oracle igényelhet egy ideiglenes munkaterületet, amelyet sikeres befejezés után eldob.
Rendszerfelügyelő folyamat (system monitor, SMON): a különböző rendszerhibák utáni helyreállítást végző folyamat. Az Oracle indításakor és befejeződésekor automatikusan elindul. Más esetben, szabályos időközönként „felébresztik”, hogy megnézze, szükség van-e rá. Ilyenkor az ideiglenes szegmensek már nem használt adatait törli. Folyamat-felügyelő folyamat (process monitor, PMON): míg az SMON a rendszerhibák után, addig a PMON a felhasználókkal kapcsolatban álló szerverfolyamatok hibái után „takarít”. Ha egy ilyen folyamat nem hajtódik teljesen végre, akkor a PMON a felhasználó megfelelő tranzakcióit, zárait és egyéb foglalt erőforrásait felszabadítja. Adatbázis író folyamatok (database writers, DBWn): a szükséges, módosított adatokat írja ki az SGA-ból a háttértárra, a megfelelő adatfájlokba. Legfeljebb 20 ilyen folyamat működhet egyszerre.
A Net8 protokoll elfedi a különböző lehetséges hálózatokat és programozói felületeket (viszony, és megjelenítési szintű protokoll). Így a Net8 illeszthető pl. IPX, SPX, IPv4, IPv6, TCP, TCPS hálózatokra egyaránt.

Relációs adatbázisok kalkulus alapú lekérdezése

Kalkulusok adottak, cél relációs Adatbázis Deklaratív lekérdezése. Csak az eredményhalmazt fogjuk jellemezni azzal. Az, hogy milyen sorrendben érjük el az adatokat, majd rábízzuk egy optimalizálási módra.
Fajták:

• Sorkalkulus
• Oszlopkalkulus

Mindkettő első rendű formális nyelv relációk leírására.
Azért, mert az eredményhalmaz is reláció lesz. Ez azért jó, mert nem kell a műveleti sorrendet megadni, csak a kívánt adatokat megadni.

Sorkalkulus

Sorkalkulus: Egy olyan formalizmus, melynek elemei megengedett szimbólumok lesznek. Ezekből a szimbólumokból atomi formulák lesznek előállíthatól, ezekből szabályok szerint formulálkat állíthatunk elő, a formulákból pedig már (Kalkulus)kifejezéseket tudunk előállítani. Ezekkel már deklaratívan tudunk lekérdezéseket csinálni.

Szimbólumok:

• ( és )
• + -
• ÉS, NEM, VAGY
• Sorváltozók s^N[j] ha j KISEBB N, amiknek N kompnensük van. j A kiválasztott komponens.
• Relációs konstansok: R^N , ez egy adatbázis táblának feleltethető meg. Lekérdezéskor ezeknek méretét állandónak tekinthetjük. N: hány halmaza van
• Exisztenciális és univerzális kvantorok. (Minden, Összes, Létezik) EXISTS, FOR ALL
• c1,c2...cn skalárok.

Atomi formula: Jelelölje R^N(s^N). Lehet egy sorváltozó és relációs konstansok. Ekkor a sorváltozók komponenseit össze tudjuk hasonlítani vagy mással, vagy konstansokkal.

Példa:

• R^N(s^N) Egy reláción N elemű sorváltozó.
• s^N[i] THETA t^N[j] (Téta= Valamilyen hasonlítási szabály)
• R^N(c1,c2,cN)
• R^N(s^N) THETA c1

Formula: Valami akkor formula, ha S^N kötött változó. Az atomi formulák mind formula. A formulákat egymással logikai műveletekkel össze lehet kapcsolni.

Létezik PSZI 1 és PSZI 2, amik formulák akkor PSZI 1 AND PSZI 2, PSZI 1 OR PSZI 2 és NOT PSZI 1 is formulák lesznek.
Ha van egy PSZI formula t szabad változója. (Ha EXISTS PSZI(t) ahol t szabad változó) Akkor:

• (EXISTS t) PSZI(t)
• (FOR ALL t) PSZI(t)

Is formulák. És ezekben t már kötött sorváltozó
Szabad: Egy változó addíg szabad amíg nem vonatkozik rá kvantor. Kötött: Egy változó kötött ha vonatkozik rá kvantor. Pl: Az egyik változóra egy kvantort alkalmazunk, akkor a változó kötött lesz. Kvantor később lesz definiálva.

Kifejezés: S^N PSZI S^N Sorkalkulus kifejezés, ha PSZI kivezetett változó az egyetlen a szabad változója, a többi változó kötött. Ez a szabad változó S^N.

Egy formális kifejezés:
{ t^(N) | PSZI (t^(N))}

Ebben a halmazban azon t értékek lesznek benne amelyekre ez a PSZI formula igaz lesz.
Ez akkor fog értelmet nyerni, ha konkrét értékeket rakunk bele ezekbe a formulákba. Logikai műveletet csak akkor lehet evaluálni, ha tudjuk a konkrét értékeket.
Példa: R^(5) (s^(5)) AND s^(5)[2] = 9 → Ahol s 2. eleme = 9
Ugyanez full formula: { s^(5) | R^(5) (s^(5)) AND s^(5)[2] = 9 } → követelmény s^(5) egyetlen szabad sorváltozónak kell lennie. Ha több van a | előtt akkor azoknak mind kötötteknek kell lennie.
Mit lehet ezzel kezdeni?
Interpretálni kell, konkrét értékekkel.
Egy értelmezés:
Vegyünk egy A számhalmazt, amibe benne van a számítógéppel ábrázolható összes szám.
c ELEMENT OF A
R^(N) SUBGROUP OF A^(N)
s^(N) ELEMENT OF A^(N) (Az A n-tagú halmazait veszik fel)
Igazságértékek hozzárendelése:
R^n (s^n) csak akkor ad igazat, ha s^n helyettesítési értéke benne van R^n-be. s^n[i] THETA t^n[j] csak akkor igaz, ha teljesül rá a THETA matematikai reláció.
Formalizmus interpretációja: Az a leírás, ahol megadjuk, hogy egy formula konstans és nem konstans változók helyére konkrét értékeket írunk. Ekkor a formulákat már el tudjuk végezni. Ennek eredményéűl a formulákhoz igazságértékeket tudunk hozzárendelni, úgy, hogy a formulákat aritmetikailag kiértékeljük. (Evaluálni)
A formulák eredménye a formulákhoz igazságértékek hozzárendelése.
E végeredmény egy olyan halmazt határoz meg, ahol a halmaznak az elemei ahol a halmaznak egy olyan M komponensű sorváltozók az elemei, ahol a halmaz elemeire kiértékelve G (formulát) feltételt akkor ez a kiértékelés igaz értéket fog adni rájuk.

Formulák logikai meghatározása

A PSZI1 AND PSZI2 pontosan akkor igaz, ha a PSZI1 és a PSZI2 is igaz.

A PSZI1 OR PSZI2 pontosan akkor igaz, ha a PSZI1 vagy a PSZI2 is igaz.

A NOT PSZI1 pontosan akkor igaz, ha a PSZI1 hamis.

A (EXISTS t) PSZI(t) pontosan akkor igaz, ha van olyan helyettesítési értéke t-nek, amire ez a PSZI(t) igaz (PSZI másik értékei mellett)

A (FOR ALL t) PSZI(t) pontosan akkor igaz, ha minden helyettesítési értékére t-nek ez a PSZI(t) igaz (PSZI másik értékei mellett)

Ezek alapján a {t^n | PSZI(t^n)} egy olyan relációt határoz meg, ahol a t n-esei a PSZI-t igazzá teszik.

Tipp: Az egy számértéket egy olyan relációnak tekintjük aminek 1 sora és 1 oszlopa van.

Tipp: {t^1 | 1=1} visszaadja a teljes érték halmazt. (ami a | előtt van az azt mondja meg, hogy a kimeneti halmaznak mennyi eleme lesz)

Tipp: {t^2 | BEVÉTEL^2(t^2)} visszaadja az összes t értékpárt, ami benne van a BEVÉTEL-ben.

Direkt példa:

• 2020 november 17.-e utáni bevételek: { t^2 | BEVÉTEL^2(t^2) AND t^2[1] = 2020 november 17.} Itt előszőr kinyerjük azokat a t-ket amik BEVÉTEL beliek és aztán szűrjük. (A bevételben a sor 1. elemei a dátumok)
• {t^2 | BANKBA^2(t^2) AND (EXISTS u) BEVÉTEL^2(u^2) AND u^2[2] = t^2[1] AND u^2[1] = 2020 november 17. } Itt egy join-ra van példa, kikeressük az u-kat és az mentén t-t szűrjük, hogy 1 dátumban mennyit raktunk be a bankba.

Gondolkozzunk el, hogy mennyire törvényszerű az, hogy akármilyen reláció algebrai kifejezést sorkalkulus kifejezéssel is ki lehet fejezni?
Ez triviálisan igaz.
E reláció algebrai kifejezés állítsa elő konstans R halmazt.
Sorkalkulusba csak ennyi: {t | R(t)} Ha tudjuk előre az outputot akkor könnyű.
De így már nem triviális: Tétel: Minden relációalgebrai kifejezésből tudunk konstruktálni egy sorkalkulusi kifejezést amely ugyanazt a relációt állítja elő mint a relációalgebrai kifejezés, és benne csak azok a konstans relációk szerepelnek melyek a relációalgebrai kifejezésben is benne van.
Bizonyítás:
Teljes indukcióval, azt kell feltételezni, hogy az n-edik lépésben E1 = {t1^(N) | PSZI1(t1^(N))} és E2 = {t2^(N) | PSZI2(t2^(N))} még nem biztonságos kifejezések. Ezután megvizsgálandó, hogy az 5 alapműveletre visszavezethetőek és adhatóak-e ezeknek biztonságos kifejezései.
Vajon fordítva igaz-e?
Nem igaz, bizonyítás: {t | NOT R(t)} (Ez egy úgynevezett nem biztonságos kifejezés
Hát ezt baromi nehéz lenne megcsinálni relációalgebrába.

Adatbázis nézetének kibővítése

Eddíg kaptunk 2 inputot:

• Kaptunk egy világ egy morzsáját, valami valakinek a fejében van, és ezt szeretnénk adatokra leképezni. Nem a teljes adathalmazt csak bizonyos adatokat.
• Megismertünk formális adatmodelleket. Példa: Objektum orientált, relációs...
  A relációs adatmodell példáúl a műveletek miatt egy keretrendszert biztosított. Az adatmodell neve egy formalizmust diktál amit mi majd egy üzleti produktumot tudunk leképezni.

(Formalizmus+szemantika.) Előmodell: Ilyen az ER modell, a világ egy darabjából egy bizonyos szemantika alapján készült modell.

Ezek kellenek ahhoz, hogy tetszőleges adatokat tetszőlegesen rendszerezve lehessen tárolni.

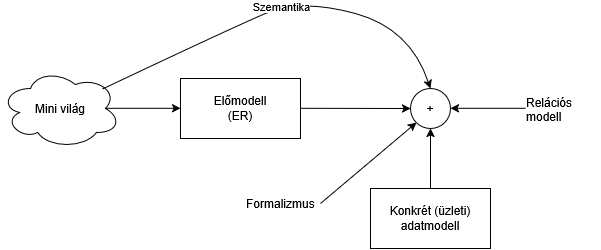
Ez ER világban 2 alapvető elem van:

• Egyedhalamzok Pl: {alma, körte, narancs}
• Kapcsolathalmazok Pl: {ide jár, innen kapja a postát}

Egy ER világban sémát úgy lehet készíteni, hogy ráhúzunk egy relációt bizonyos attribútumokkal, melyek 1 konkrét sort képeznek le.
Pl: Ember(név,életkor,TAJ szám)
Legyen egy R ternáris reláció, ami A, B, C egyedhalmazokat csatol össze.

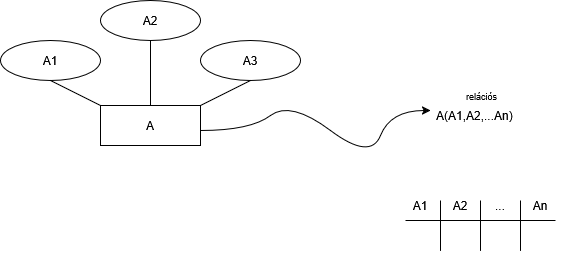
Ezeknek az A,B,C[1,2...n] halmaz elemeinek kell egy sémát definiálni.
De hogy nézzenek ki az elem sémáinak attribútumai?

Legyen egy A1,B2,C3 elem, és ezeknek jelezni kell, hogy összetartoznak.
1 elemet úgy tudunk azonosítani, hogy a1,a2...an attribútummal hivatkozunk rá, ez egy A[a].-ik elemét fogja azonosítani.
Ez alapján azonosítsuk a B és C halmaznak egy elemét:

a1...an,b1...bn,c2...cn
Ez azonosításra jó, de nem a legjobb. Jelzi, hogy az adatok egybe tartoznak de redundánsan tárolja őket.
(Lásd: Később funkcionális függőség és normalizálás)
Nem kell az egyik egyed összes attribútumait felsorolni, van olyan, ahol 1 attribútum is egyedileg megkülönböztet minden tagot. (Ismétlésnek ez a kulcs)
Legyen A, B és C kulcsai A[i], B[j] és C[k].-ik attribútumai.
Ekkor jelölhetjük R'(A[i],B[j],C[k]). Itt látható, hogy ez elégséges annak a jelzésére, hogy egy A, egy B és egy C beli elem valamilyen attribútum mentén kapcsolódik.
De ezek nem a relációban kulcs, mert ezek az A, B és C sémában kulcs. Ez egy idegen kulcs.

Idegen kulcs: Egy kapcsolótábla vagy egy egyedi kulcs, ami összekapcsol N tábla mentén példányokat. Csináljunk egy kapcsolótábla:

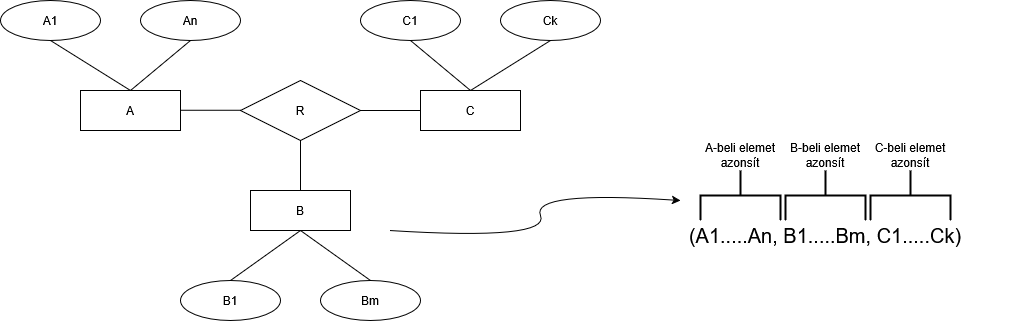
Kapcsolat azonosítók
a1,a2...an	b1,b2...bn	c1,c2...cn

Hát ez így nem a legjobb. Nem ad egyértelműséget. Lehet N-to-N-es viszony is.
Más tipp:
Ha A-ból csak 1 B értéket lehet elérni, akkor vegyünk fel A-ba egy attribútumot, ami alapján egyértelműen lehet azonosítani egy B beli elemet.
Pl: Ha B emberek, és B-ben van egy név, akkor A-ban felvehetünk egy ember név nevű attribútumot. Így az A-beli elemek tudni fogják, hogy melyik B tartozhat hozzá.

Fizikai adatszervezés

A lényege, hogy az adatbáziskezelőnk egy operációs rendszer felett ül, mint alkalmazás és használja az OS fájlrendszerét.

Fájl: Egy olyan konstrukció, amely képes adatokat perzisztensen tárolni. Figyelembe kell venni, hogy rekord-szerű struktúrákat akarunk a fájlokba tenni.
Ilyenkor blokk-orientált háttértárat feltételezünk.
De mit is jelent ez pontosan?
Hogy nem karakter szinten tudjuk bevinni az adatokat, hanem blokkosítva, akár 4096 darabot is, ha 1 blokknyi adat = 4096 egység.
Mindíg konkrét blokkok utaznak az operatív és a háttértár között.
Az operatív tárból mérnöki becsléssel (mostani technológiákkal) általába 4-5x gyorsabb az adat kezelése.
4 alapművelet a rekordszerű struktúrákkal:

• Keresés
• Törlés
• Beszúrás
• Módosítás

blokk-orientált háttértár:

• HDD
• SSD

Ezeket ilyen módon lehet majd kezelni:

• Heap (nem a C-s heap)
• Hash
• Indexek

Heap: Ez egy formája a fájl állományok szervezésének. Ez akkor jellemző, ha semmilyen segédstruktúrát nem használunk rekordjaink tárolásához. Veszünk 1 blokkot minden rekordnak.
A blokkokban mindíg csak egész számú rekordot helyezünk. Szóval 1 rekord max 1 blokkon lehet, és mondjuk 1 blokk X rekordot képes tárolni. A blokk mérete (2025-ben) tipikusan 512byte-64KB lehet.
Blokk:

Head	Blokk tároló egysége
Láncolás, adatok a blokkokról, mennyi szabad, stb...	b1,b2...bn

A blokkméret adott, és a b1,b2...bn rekordok egyforma hosszúak.
Ha ezeknek adott a mérete, akkor az esetek többségébe a blokkokban lesz majd mindíg valamennyi byte, amit mivel adott mennyiségű egész mennyiségű rekordot tárolunk, nem tudunk felhasználni.
Ezt le kell nyelni.

Egy rekord így nézhet ki:

Header	Mező 1	Mező 2 (hosszabb, mondjuk 1024 hosszú string)	Mező 3...

Műveletek heap-en: (Egy ember sémával)

• Keresés: Ki akarjuk az egyik rekordot olvasni, úgy, hogy tudjuk, hogy Gipsz Jakabot keressük. Akarjuk, hogy hányas lába van. Ezt fáradtságosan fogjuk megtalálni. Előszőr meg kell találni, hogy a rekord melyik file-ba van. Valamilyen módon ezt azonosítani kell. (Az adatbáziskezelő ezt megmondja) Ha ismerjük ezt a file-t akkor az OS-nek mondani kell, hogy adja oda az 1. blokkot. Az 1. blokkművelet baromi hosszú idő lesz, mert még nincs a háttértárba. Ezek után a rekordokat ki kell keresni. De honnan tudjuk, hogy a rekordban mi a kulcs? Ez a metaadat tárban benne lesz definiálva.
  Az alapján ki tudjuk számolni a kulcs hosszát, offsetjét és megnézhetjük, hogy megegyezik-e Gipsz Jakabbal, ha egyezik, akkor jó. Ha nem akkor megyünk a 2. blokkba. A lényeg az, hogy egy exhaustive keresést kell blokkonként és rekordonként végezni. Mindegyiket meg kell nézni. A blokkon belüli keresés ideje elhanyagolható.
  Ez lineáris keresés, ha N blokk van és M rekord, akkor minimális blokkműveletszám: 1, átlagosan: (1+N)/2, ez O(N) algoritmus lesz.
  Az Oracle is ezt használja
  Pozitívumok:
  • Olykor nagyon nagy overheadja lenne, ha extra adatok alapján azonosítanánk és keresnénk a rekordokat.
  Negatívumok:
  • Lassú.
• Törlés: Előszőr ki kell keresni, ez O(N) (N = blokkok száma). A rekordok elején van egy bit, hogy törölve van-e. Ha ezt 0-ról 1-re rakjuk akkor jelezzük, hogy ezt a blokkot töröltnek tekintjük és ide majd egy másik blokkot vagy rekordot tudunk tárolni. Törlés ténye nem véglegesedett ezzel, mert az adatbázis diszkrezidens és csak az operatív tárba "töröltünk". Nem véglegesítettünk semmit.
  Ezt a rekordot vissza kell írni a háttértárra, de 1 bitet nem tudunk írni, mert blokk-orientáltan működünk. 1 bit miatt lehet, hogy 32KB-ot írunk a disk-re. Visszaírás: +1 blokkművelet. O(N)
  
• Beszúrás: Kell vizsgálni egyediséget? Ha igen és nincs segédstruktúránk, akkor végig kell nézni az összes blokk összes rekordját, ez már alapból O(N) N blokkméretnél a keresés miatt. Meg kell keresni, hogy már van-e benne. Ezt más módon is lehet biztosítani (ROWID vagy egy auto-increment kulccsal). Ha nincs benne, akkor lehet írni az új rekordot. Ezt egy üres helyre vagy egy fájl végére be lehet írni. Az üres helyeket, ha volt eszünk még az előző kereséskor kijegyeztük az üres helyeket. Ilyenkor a beszúrás +1 blokkművelet + keresés: O(N)
• Módosítás: Gipsz jakabnak megnőtt a lába, módosítani kell. Ilyenkor ki kell keresni és írni kell, +1 blokkművelet + keresés: O(N). Az is lehet, hogy a nevét változtatta meg. Ilyenkor ki kell keresni, hogy van-e már ilyen, ettől függetlenül ugyanúgy O(N).

Látszik, hogy minden a keresés sebességétől függ. Ha gyorsítani akarunk akkor a keresést kell felgyorsítani.
Csavar erre: használjunk hash szervezést!
Hash: Egy olyan szervezési forma ami használ egy hash tábla segédstruktúrát. Ezek pointereket (mutatókat) tárolnak, amibe B számú bejegyzés van. (vödrös hash-t használunk elsősorban). A H hashfüggvényünk olyan, hogy leképezi a rekordok helyét [0,1 (max fájl méret)] intervallumra. Itt most a blokkokhoz egy segédstruktúrákon keresztül tudunk hozzáférni és a blokkláncokat elérni. (A vödrös hash miatt) A vödrös láncolást a blokkok header adatában el tudjuk láncolt lista formációban tárolni (előző blokk, következő blokk). Ha a H hash függvény egy k kulcsértékű rekordot a H(k) helyre képez le, akkor a hash tábla megmondja, hogy a k kulcsértékű rekordnak melyik vödörbe kell lennie. Jó hashfüggvénynél a vödrök egyenlegesen fognak nőni.

1 vödörben ekkor várhatóan N/B blokk lesz. Ez keresési időben, ha B elég nagy csökkenést fog eredményezni. Ha B=N, akkor a keresés 1 blokk műveletet fog (perfekt hash függvénnyel) igénybe venni, és így a keresés minimum 1 blokkművelet: O(1). Ez a leggyorsabb blokk-orientált háttértárban. Gyakorlatban, ez az operatív tár méretétől függ, B nem lehet nagyon nagy. 1 mutató 1 bájt (minimum), gazdaságosan az operatív tárból egy milliómutató 8MB hely. Szóval kevés. Egy nagyon alap RAM 4GB méretű. Ez ennek RAMnak a töredéke. Ezek elég olcsóak így nagyon sokat nyertünk nagyon olsóan.

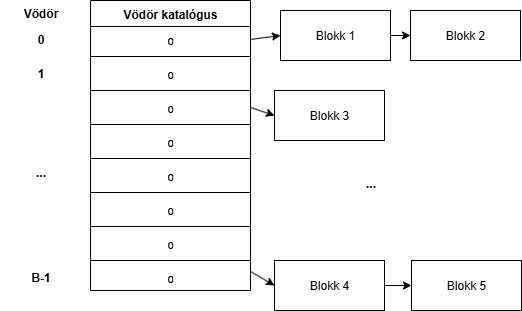Műveletek a hash-el:

• Keresés: O(N/B) 1. Megkeressük a rekord Kulcsát, majd h(K)-t kiszámítjuk és a vödör h(K).-adik bejegyzéséből kiolvassuk az adatot. (Ha benne van az adatbázisban akkor csak itt lehet)
• Törlés: O(N/B) Lásd: Heap művelet +- a jobb keresés. Itt elég csak a törölt bitet átállítani.
• Beillesztés: O(N/B) Lásd: Heap művelet +- a jobb keresés.
• Módosítás: O(N/B) Lásd: Heap művelet +- a jobb keresés.

Az indexelésről

Index: Ennek a szervezésnek az a speciális tulajdonsága, hogy blokkszervezésű és ebbe az állományba index-rekordokat tárol. Egy index-rekord egy kulcs értéket és egy mutatót tartalmaz a rekordra. Az index állomány a kulcs érték szerint rendezett lesz (mindíg). Lehet itt már bináris keresést használni.
Műveletek a hash-el:

• Keresés: O(log2(N+1)) Egy adott kulcs érték alapján bináris keresés. Mivel rendezettek kulcs alapján a rekordok így használhatunk bináris keresést.

2 féle indexelést ismertetünk:

• Ritka index: Jóval kevesebb az index rekordok száma az aktuális rekordok számánál.
• Sűrű index: Az index rekordok száma majdnem megegyezik a rekordok számával.

ISAM: Az index rekordok száma megegyezik a rekordok számával. Felmerül a kérdés, hogy ha kevesebb az index rekord, akkor honnan a fenébe tudom, hogy melyik rekord hol van.
Megoldás: A blokkokban is a rekordokat is kulcsérték szerint rendezetten kell tárolni.
Példa: Olyan mint egy nyelvi szótár, ha tudjuk, hogy rendezettek, akkor a Zebra jelentését nem a könyv elején keresem, hanem a Z betűs szavaknál.
Az ISAM-kor a keresés:

• Keresés: O(log2(X)) Ahol X az index rekordok között ugrálásának száma.

Forumla doménje: Formálisan a DOM(PSZI) = { olyan halmaz, aminek a formulában talált konstans relációknak és értékei (skalárjai) a tagjai} Ilyen konstans, ami Pl: Szeptember 15.-es Biztonságos sorkalkulus kifejezések: Egy sorkalkulus kifejezés biztonságos, ha a tartalmazott elemeit egy az interpretációs halmaznál kisebb halmazra megszorítva is értelmes eredményt kapunk. ez a formula doménje. Ez azon értékek halmaza, amik az adatbázisban ténylegesen reprezentálva vannak. Pl: Az ember tábla életkor mezője. Formálisan: Az adott változókhoz tartozó megfelelő helyettesítési értéket keresünk. Egy formula biztonságos akkor, ha a PSZI(t) formulában a szabad változót igazzá tevő összes t helyettesérti érték ELEMENT OF DOM(PSZI). Az összes OMEGA(u) helyettesítési érték DOM(OMEGA).
Tétel: Minden biztonságos sorkalkulusi kifejezéshez található egy relációalgebrai páros. Ez fordítva is igaz.

Oszlopkalkulus

Csak a használati formalizmusban különbözik.
Elemei:

• s^(n) helyett X1,.. Xn
• R^(n) (t^n) helyett R^n(X1,X2,...Xn)
• Xi THETA Xj
• R^n(c1,c2,...cn)
• Kifejezés: {X1,X2,Xn | PSZI(X1,X2,Xn)} lehetnek kötött konstansok.

Mintaképpen itt van pár lekérdezés oszlopkalkulussal:

• Szeptember 15.-i árbevételek: { x,y | BEVETEL(x,y) AND x > 2020-09-05} (X = dátum, Y = bevételek), beszédes nevekkel jobb:
• Szeptember 15.-i árbevételek: { datum,bevetel | BEVETEL(datum,bevetel) AND datum > 2020-09-05}
• Itt egy másik: { összeg, befiz| BANKBA(összeg, befiz) AND (EXISTS datum) BEVETEL(datum, osszeg) AND datum = 2020-15-20 }

Ez a lekérdezéseknek egy elegánsabb formalizálása.

2. Labor fontosabb fogalmak

Ezeket a fogalmakat a labor előtt érdemes ismerni:

• Adatbázis séma
• Relációs séma
• EER (Extended ER ) model
• Fogalmi adatbázis (logikai)
• Reláció fokszáma
• Relációalgebra
• kulcs

Tipp: A relációalgebrai szelekció az SQL WHERE-clausenak felel meg, míg a Projekció a SELECT-nek.

Fizikai adatszervezés 2.

Egy sajátos, limitált modellben dolgoztunk. Nem mindenre jut idő, nem mindent írtunk le rendesen.
Így kell az adatszervezést (fizikait) elképzelni: Az adatbázis szeretne valamit tárolni: "Plíz daddy oprendszer, kérek blokkot!". Ezek után valamennyi idő után az adatblokk megérkezik.

A lényeg az, hogy ezt a várást ki tudjuk használni addíg másra.
A nem felejtő háttértár kezelése sosem közvetlenül valósul meg, egy fájl interface alapján lesznek az adatok tárolva, előírva.
Amikor a 3 rétegű modellről beszéltünk, akkor az alsó réteget még fizikai struktúrának hívtuk. Most már állományszervezésről is beszélhetünk. Csak azt akarjuk megmondani, hogy az adatokat hogyan, és milyen adatokat tároljuk el, nem akarjuk azt megmondani, hogy hol.
Nem triviális, hogy a fájlokat milyen sorrendben tárolják az adott alsó rendszerek.
A fájljaink blokkokat tárolnak (egész számú mennyiséget), a blokkok pedig rekordokat. Ezen felül fontos megjegyezni a 3 előbbi megismert módszert.
Emlékeztető: A hash elég hatékony módszer tud lenni bizonyos tényezők mellett, lásd fentebb.
Az indexeket képzeljük el valamilyen háttértáron elhelyezkedő struktúrának.
Ha az indexek rendezettséget biztosítanak, akkor hiba lineáris keresést használni. Használjunk bináris vagy interpolációs kereséseket!
2 féle index van, a ritka index és a sűrű index. Ha mi sokkal kevesebb index rekordal akarunk sokkal nagyobb halmazba keresni, akkor ide ki kell valamit találni.
Megoldás: Az adatállományt is kulcsérték szerint kell tárolni és rendezni. Ez az ISAM keresés, alapvetően log2(M)-el lesz arányos, ahol az index állomány blokkjainak a száma az M. Ahol definíció szerint az index állományban az indexrekordok száma megegyezik az adatállományban lévő rekordok számával. Tudjuk azt is, hogy ha egy meghatározott helyen egy index alapján nincs keresett adat, akkor tudjuk, hogy máshol se lehet, mert az index akkor azt mondta volna.

Példa: Egy szótárba addíg keresünk, amíg megtaláljuk azt a szót, ami kisebb betűvel kezdődik lexografikusan, mint a keresett szó. Ha ezt megtaláljuk, akkor tudjuk, hogy az után lesz a keresett szó.

ISAM-al beszúrás

Nem triviális, olyan, mint ha egy teli szótárba akarunk adatot berakni.
Mit lehet csinálni? Azt az oldalt ahova be kell szúrni, ki kell tépni, kell venni 2 oldalt, mindegyikre a felét rárakjuk az eredeti lapnak, így lesz hely.
Ez a blokkhasítás. Ekkor az indexállományt is frissíteni kell. Keletkezett egy új blokk, ennek keletkezett egy új index rekordja, ezt az indexet be kell szúrni az állományba.

Fontos: Az indexnek mindíg rendezettnek kell lennie. Ha nincs hely az indexállományba, akkor itt is block splitet hajtunk vége. Ezek után frissíthetjük az index állományt.

Törlés ISAM-al

Triviális, be kell állítani a törölt biteket. Viszont ha sok a törlés, akkor a régi adatok, amik már töröltek foglalják az indexeket és a tárhelyet. Az indexstruktúrát is frissíteni kell időnként vagy mindíg.

Feloldás: A szomszédos blokkokban hány olyan blokk van, ami még él? Ha kevés, akkor block splittelünk. A még élőeket egy új oldalra rakjuk, a többit kidobjuk. Így az indexállományt is frissíthetjük. Ekkor ennek a mérete is fog csökkenni.
Ennek a részletei már implementációs kérdés.

Módosítás ISAM-al

Ha a módosítás a kulcsot is érinti, akkor baj van. Ilyenkor a célszerű eljárás a törlés és beszúrás.

Keresés ISAM-nál

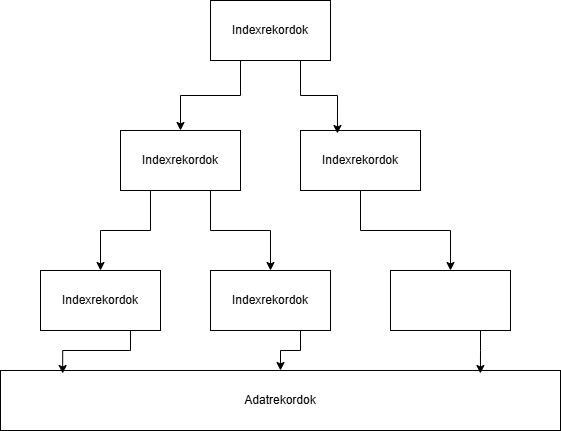Itt az indexek között a bináris keresés elég optimális. Viszont a log2 keresés is növeli a többi parancsnak is a végrehajtási idejét.

Mit lehet ilyenkor csinálni? Észre kell venni, hogy a fájlok rendezettek. Azokban is lehet keresni és sokkal gyorsabban is. Az embernek lényegesen kevesebb blokkot kell átnézni.
Ezt el lehet sütni az index rekordokra is. Csinálni kell egy index rekordod ami az előző index rekord egy blokkját címzi meg.
Ezt el lehet sütni, lényeg az, hogy a végén 1 blokk legyen, ekkor ebből egy fa struktúra lesz:

Ekkor az 1 magányos blokk a gyökér, az adatblokkok meg a levelek. Innentől kezdve a keresés logikája már meg fog változni.
A keresés innentől abból fog állni, hogy mindíg elindulunk a gyökérből. Meg keressük a következő index rekordokat, ahol a legkisebb kulcsérték még kisebb, mint a keresett index. Ezek után beleugorhatunk rekurzívan a következő index állományban és ismételhetjük ezt. Addíg megyünk míg blokkot nem találunk vagy találjuk, hogy hiányzik a bázisból.
Ez egy kiegyenlített fa. Ekkor a keresés annyi művelet, mint ahány szint van. logK(M) lesz, ahol k az index rekordok száma egy állományba.

Az a K lehet akár 100 is nagyságrendileg.
Fontos: A kiegyenlítettség elvárás. Fontos erre figyelni, hogy ezt ne sértsük.
A beszúrásnál lehet, hogy a fa magasabb lesz, máskor lehet, hogy 1 törlés 1 egész szintel csökkenti a fát.
B* fa = Bayer kutató írta le.

Sűrű indexek

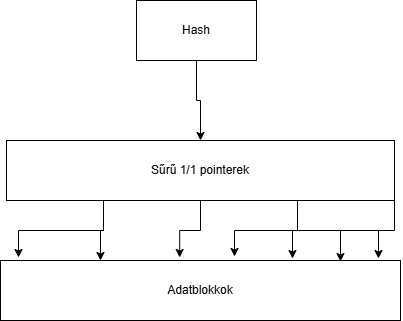
Minden adatrekordhoz létrehozunk egy indexrekordot. Ennek tetejére rakhatunk egy hash-et, amivel el lehet érni a sűrű index rekordok állományát.
Hátrány: garantált +1 blokkművelet. Ráadásul ennek + háttértár is kell. Ennek tetejére ezt az indexstruktúrát is módosítani kell, ha módosítjuk a tárolt adatrekordokat (+karbantartási igény).

Ez egy látszólagos vesztett helyzet, de azért ennek sok előnye is lehet.
Ha minden egyes adatrekordhoz tartozik egy indexrekord, akkor az a logika, hogy az adatállományt rendezetten kell tartani, az felesleges. Akárhová beszúrhatunk egy rekordot.
Ha nem kell rendezetten tárolni, akkor van egy olyan előny is, hogy a kitöltöttség magasabb lehet, nem lesz redundáns adat a felezett blokkoknál.
Sokkal jobban tudjuk a háttértárat kihasználni.

Gondoljunk bele abba, hogy ha ritka index alapon szeretnénk egy állományt több mező alapján is indexelve keresni. Akkor ott bajok vannak, kell mégegy külön index.

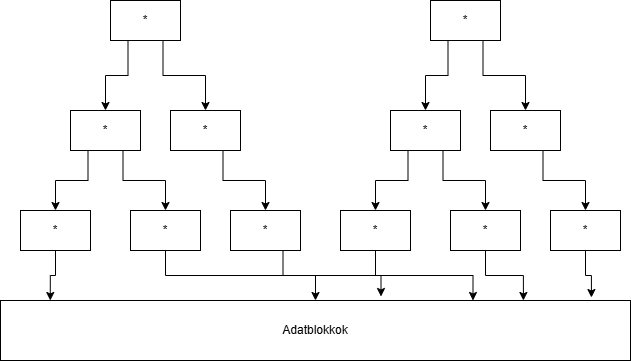
És akkor is ha van, akkor az adat rekordokat csak egyféleképpen lehet rendezni.
De ha személyi számra vannak az emberek rendezve, akkor adószám index alapján hogy találunk meg akármit is, hisz nem alapján van rendezve.
Megoldás: Sűrű indexet berakni a ritka index B* fa alá, ekkor az adatállománynak nem kell rendezettnek lennie és ebből azt nyertük, hogy több indexünk is lehet.
Ezt az adatrekordba akárhány indexre meg lehet csinálni, csak annyival több sűrű index + B* fa fog kelleni.


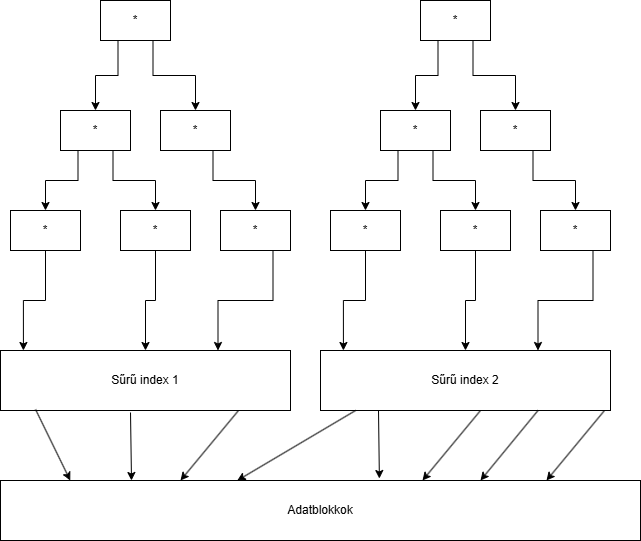
Ahhoz, hogy érdemben tudjunk haladni, a kulcs jelentését egy kicsit át kell szemantikailag definiálnunk.
Fizikai kulcs: Általánosabban kulcsnak nevezünk egy olyan mezőt, ami alapján keresünk. A keresés eredménye itt nem lesz feltétlenül egyedi. Pl: Kik a kecskeméti lakosok? A Kecskemét, mint város lesz a kulcs, a találat 70000 lesz, mert annyian laknak ott. Itt az egyediséget senki nem követeli meg. Mit veszünk észre? Annak ellenére, hogy +1 blokkműveletet kapunk, ez gyorsabb lesz, mert nem kell rendezve beszúrni és törölni se. A keresés ideje a felső szintektől függ. A sűrű index blokk overheadja sokkal kisebb, az iteráció lényegesebben kevesebb blokk között kell, hogy lefusson.
Ebből az fog kijönni, hogy bőven megnyerjük a +1 blokkművelet overheadjét általánosságban.
A gyakorlati megvalósításban a sűrű index mindíg ott van a ritka index és az adtállományok között.

Relációs lekérdezések optimalizálása

Általánosságban, arról beszélünk, hogy valaki valamilyen módon megfogalmazta azt, hogy mit szeretne lekérdezni az adatbázisából (akár deklaratívan).
(Lásd, oszlopkalkulus, nagyon direkt módon fordítható le az SQL SELECT utasításra.)
Ezen keresztül válik az Oszlopkalkulus teljessé.
Ezt a lekérdezést sokféleképpen lehet leképezni. Relációalgebra segítségével is már többféle képpen le lehet írni 1 olyan lekérdezést. Nagyon nem mindegy a sorrend, mert overheadba és gyorsaságba nem mindegy, preferáljuk a gyorsabb lekérdezéseket.
Az sem mindegy, hogy egy szelekciót milyen indexre csináljuk.
Irgalmatlan sok kombináció van, ha a műveletsorrendeket nézzük. Lehet 2 olyan művelet, ahol az egyik másodpercek alatt fut le, a másik napok alatt, de mind kettő ugyanazt csinálja.
Az sem mindegy, hogy az adatbázis rendszer hogyan működik.

2 féle alapvető módszer létezik, de ezenkívűl nagyon sok más. Ezek az optimalizálások sokváltozós, lineáris térben végezendők.

Heurisztikus szabály alapú optimalizáláss

Optimalizálás: Egy lekérdezés módosítása úgy, hogy az gyorsabb legyen és a végeredmény ne változzon meg. Ezt műveletek módosításával tudjuk elvégezni.
Egy olyan dolog, ami megmondja, hogy milyen műveletet, milyen sorrendben, milyen algoritmusokkal, milyen workflowba kell előállítani a végeredményt. Imperatív megfogalmazás esetén is lehet optimalizálni.

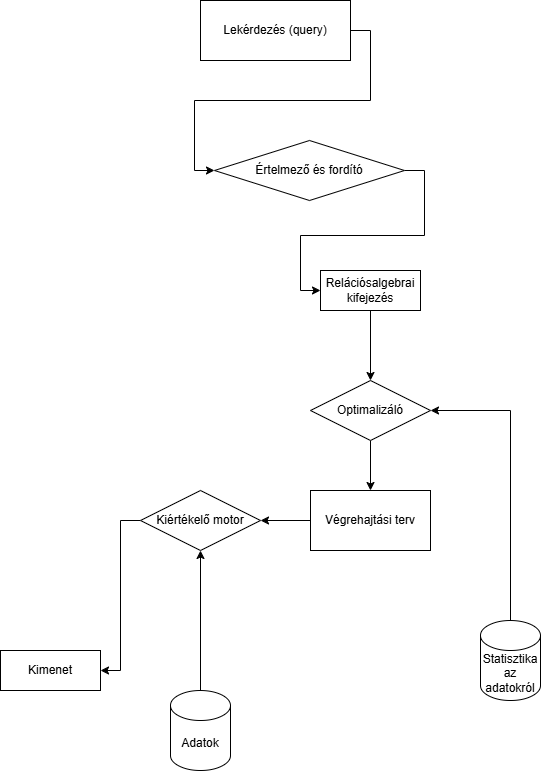
A heurisztikus optimalizálás alapja az, hogy egy reláció alapú fa transzformációját kell előállítani.
Ez a fa egy lekérdezés. Példa:
ALKALMAZOTT(id,csaladi_nev,keresztnev,szuldatum)
PROJEKT(p_id,nev)
EZEN_DOLGOZIK(project_id,employee_id)
Ekkor ilyen lekérdezést lehet csinálni:
select csaladi_nev FROM alkalmazott, ezen_dolgozik, projekt where employee.szuldatum > '1997-12-31' and ezen_dolgozik.project_id = project.id and ezen_dolgozik.employee_id = alkalmazott.id and project.nev = "Hepenix"; No, akkor most hogyan?Ábrázoljunk egy adott relációalgebrai kifejezést, ahol definíció szerint a fa gyökerében az eredményhalmaz van. A fa levelei az input reláció, amin dolgozik a lekérdezés. A fa csoportjai a műveletek. A vonalak, pedig azt mutatják, hogy miféle inputreláción keresztül kell az adott műveleteket elvégetni:
PROJECTION csaladi_nev (SELECTION szuldatum>'1997-12-31'(employee) NATURAL JOIN ezen_dolgozik NATURAL JOIN (SELECTION project.nev = "Hepenix" (project)))
A képen látható egy reprezentáció: (Az egyszerüség kedvéért az E fogja az employee-t, a P a projekteet és a W (works_on) az ezen_dolgozik-at.

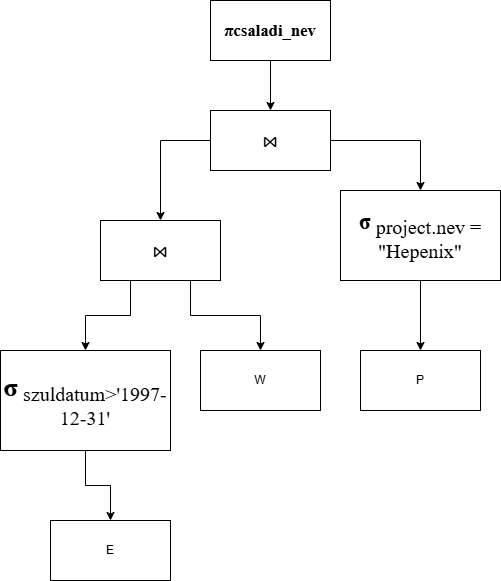
Cél: A leggyorsabb alak kiválasztása.
Hogyan kell ezt végrehajtani? Azért, hogy reprodukálható legyen az optimalizálás, dokumentálni kell a kezdő alakot.
Kanonikus alak: Megcsináljuk a descartes szorzatokat, majd a szelekciókat, majd a projekciókat. Ezek után a szelekciókat le akarjuk nyomni a lehető leglejjebb az inputrelációkhoz közelebb. Miért is? Azért, mert a szelekció miatt kevesebb adattal kell majd tovább dolgozni. Azért jobb ezeket lenyomni, hogy ezek a szűrések minél hamarabb elkészüljenek.
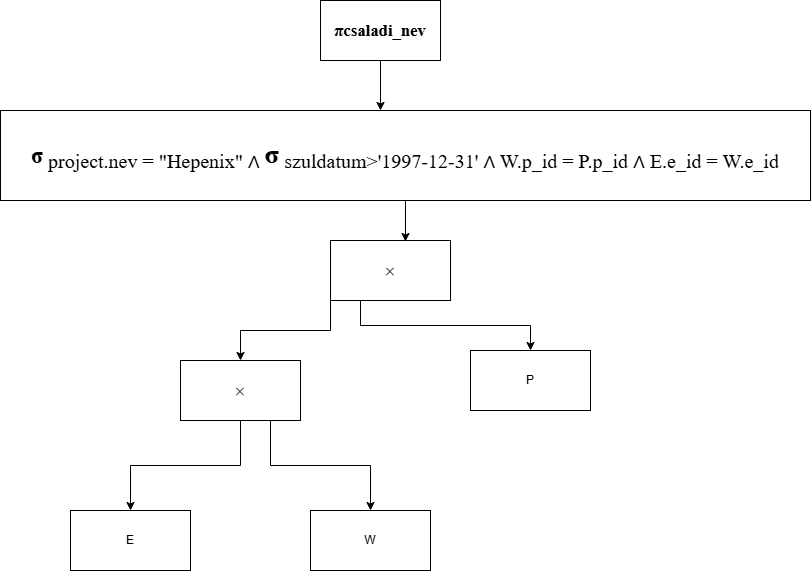Következő lépés: Ha lehet, akkor rendezzük át a leveleket. Az előző részben az employee.ezen_dolgozik táblát descartes szoroztunk az alkalmazottak táblával. Na, ha ezek nagyon nagyok, akkor ennek nagy overheadja lesz.
Fogjuk magunkat és az ezen_dolgozik táblát a szűrt projekt táblával descartes szorozzuk, ekkor a szűréssel már csak az a projekt fog szerepelni, descartes szorozva nem lesz annyira nagyobb: Y*1 = Y.
Ez nem fogja megváltoztatni a végeredményt, mivel független a 2 szelekció.
Ilyen minta lesz: descartes után szelekció, descartes után szelekció,...
Látható később, hogy ha ezeket egy műveleteknek tekintjük akkor jobban lehet őket optimalizálni. (Equi-join-okkal)
Végül a projekciókat is meg kell próbálni süllyeszteni. Végül csak a családi név kell, a többi projekciókat ki is hagyhatjuk. Ezt egy közbülső projekcióval lehet megcsinálni.

Ekkor megkapjuk a heurisztikus szabályon alapuló optimumot. Determinisztikus lesz, mert mindíg ugyanúgy csináljuk és emiatt heurisztikus is lesz.
Ez egy "gyorsabb" optimalizálás volt. Ha a bonyolult optimalizálás tovább tart, mint ha csak az eredeti lekérdezést futtattuk volna, akkor feleslegesen optimalizáltuk.
Főbb kérdés: A fa transzformációkat mikor is lehet elvégezni?
Azonosságok:

• SELECTIONTHETA (E1 DESCARTES E2) = E1 NATURAL JOINTHETA E2 (A szelekció konjuktív elemeit kaszkádosíthatjuk is, Példa: Nem mindegy, milyen sorrendbe dobálunk ki adatokat?)
• E2 NATURAL JOINTHETA E1 = E1 NATURAL JOINTHETA E2 (Lásd, eggyel felső lista elem magyarázata.)
• (E2 NATURAL JOINTHETA1 E1) NATURAL JOINTHETA2 E3= E1 NATURAL JOINTHETA1 (Kommutativitás és disztributivitással is rendelkezik)
• SELECTIONTHETA1 (E1 NATURAL JOINTHETA2 E2) = SELECTIONTHETA1 (E1) NATURAL JOINTHETA2 E2
• PROJECTION L1 UNION L2 (E1 NATURAL JOINTHETA1 E2) = (PROJECTION L1(E1)) NATURAL JOINTHETA1 (PROJECTION L2(E2)) (Ez azt mondja, hogy van egy egymásba ágyazott projekciós lista, a relációt különbőző attribútumokra vetítjük, ez megegyezik azzal, ha a relációt csak a legkülső attribútumlistára vetítjük, ez igaz, de csak akkor, ha az alap egyenlet szintaktikailag helyes. A listában nem lehet olyan attribútum felsorolva, ami a későbbi bennelévő relációban nem található meg. Szóval felesleges cím alapján filterelni, ha egy sor nem is tartalmaz címet, mert már mondjuk el lett hagyba)
• (A vetítés és a szelekció felcserélhet, megint csak akkor, ha a 2 oldal szintaktikailag helyes.)

Költségalapú optimalizálás

Ez egy bizonyos szélsőérték számítás. Itt is sok kompromisszum lesz, de egy teljesen más megközelítés. Sokkal többet kell számolni.
A számítógépek kapacitása nőtt, így már más, komplexebb algoritmusokat is tudunkk használni.
Fontos, hogy leginkább akkor éri meg optimalizálni, ha egy Lekérdezésről tudjuk, hogy sok ideig fog tartani vagy sokan használják azt a lekérdezést.
Végrehajtási terv: Az tartozik hozzá, hogy milyen műveleteket, milyen sorrendben, milyen algoritmusok szerint, milyen workflowban hajtunk végre. Ezek mindegyike befolyásolja valamilyen költségbe a végrehajtás idejét Operatív metaadat: Egy táblában való adatokról mond el valamit. Pl: Hány sor van itt? Hány oszlop van?... stb. Katalógusadatok: Az adatbázis és táblához tartozó pillanatnyi adatot. Pl: Indexek, adatok eloszlása, milyen adat van benne. Ilyenek a struktúrális metaadatok, szemantikus és operatív metaadatok. Fontos, itt becsülni fogunk (méghozzá durván), hogy milyen költségekkel kell számolni.

Változó hosszúságú rekordok kezelése

Változó hosszúságú rekordunk lehet, ha egy mező hossza változó vagy ismétlődő mező / csoport van a rekordban. (Inkább hálós adatbázisra jellemző)
Erre ismerünk pár megoldást. A változó hosszúságú adattagokat a rekord végére rakjuk, így az eleje a rekordnak mindíg fix.

Egy másik megoldás, a pointerezés. A változó adat helyett egy fix méretű pointer van ami egy másik állományba tárolt adatra mutat.

A 2. esetet kicsit több módon tudjuk feloldani, minden módszernek vannak előnyei és hátrányai:

• Lefoglaljuk azt a helyet, ami a maximális ismétléssel vett hely lenne. Ez nyilván pazarló is lehet.
• Pointerezünk, ebben az esetben egy táblára előszőr és onnan az ismétlődésekre is pointerezünk.
• Kombinált, hibrid módszer: Lefoglalunk valamennyi helyet, ha az nem elég akkor pointerezünk.

Szimbólum katalógus:

• n_r: Az r relációban lévő rekordok száma.
• b_r: Az r relációban levő rekordokat tartalmaző blokkok száma.
• s_r: Egy rekord nagysága bájt-ban.
• f_r: A r relációban mutatja, hogy 1 blokkban hány rekord fér el. (Ez a blocking factor.)
• V(A,r): Hány különböző érték fordul elő az A attribútumokban az r relációban. (Ezt az attribútum kardinalitásának is nevezzük). V(A,r) = PROJECTION A(r)
  Ha A egyedi, akkor az attribútum kardinalitása meg kell egyezzen a rekordok számával.
  Ha A kulcs, akkor V(A,r)=n_r
• SC(A,r): Selection cardinality. Egy adott attribútumon feltétel szerint megfogalmazunk egy vagy több kiválasztási feltételeknek. Ez azt jelöli, hogy ezeknek a kiválasztásnak átlagosan hány rekord fogja kielégíteni a feltételeket.
  Ha A kulcs, akkor SC(A,r) =1, mert 1 kulcs érték egyezhet. SC(A,r) = n_r / V(A,r)
• Blokk faktor = rekordok / blokkok ALSÓ EGÉSZ RÉSZE.
• f_i: A kimenetek átlagos száma, egy fa egy adott csomópontban legfeljebb hány helyre tud elágazni.
• HT_i: Az index szintjeinek száma: HT_i = logf_i(V(A,r) B* fánál. HT_i = 1 definíció szerint, ha van hash tábla és úgy érjük el a rekordokat.
• LB_i: A levélszintű indexblokkok száma. Ez változó hosszúságú rekord. (Lowest level index Block)

Költség meghatározása

Miben mérjük a költséget? Mit akarunk optimalizálni?
Ennek meghatározása: (teljesség igénye nélkül)

• Blokkművelet számban?
• Válaszidő alapján?
• Kommunikáció alapján? (Pl: Elosztott rendszerben.)

Költségfüggvény: Háttértár blokkolvasások és írások száma a válasz kiírásának költsége nélkül. Ezt akarjuk minimalizálni. Ekkor egyes operátorok költségének összege.

Operátorok, műveletek költsége

Estimation: Egy művelet költsége. Jelölése A1 művelettel: E_A1 Select

• A1: Lineáris keresés, E_A1 = b_r
• A2: Bináris keresés, (renezettség szükséges a A attribútum szerint, folyamatosan helyeszkedjenek el a diszken) E_A1 = $$\lceil {log}_2\left(b\mathrm{_r}+1\right)\rceil +\lceil \frac{SC(A,r)}{fr}\rceil -1$$

Elsődleges index: Elsődleges index az, ahol ha sorba megyünk akkor az adatrekordokat az ő fizikai tárolási sorrendjükbe tudjuk elérni. Indexelt szelekciós algoritmusok:

• A3: Elsődleges index használatával egyezés keresése. E_A3 = HT_i+1
• A4: Elsődleges indexel való keresés, ahol nem kulcs attribútumon nézünk egyezést. E_A4 = $$HT\mathrm{_i}+\lceil \frac{SC(A,r)}{f_i}\rceil$$
• A5: Másodlagos index használatával, egyenlőségi feltétel mellett.
  E_A5 = HT_i + SC(A,r) ha A nem kulcs.
  E_A5 = HT_i+1 ha A kulcs. Be kell járni a fát, hogy megkeressük a jó blokkokat + hány helyre kell elmenni az SC(A,r) ezt megmondja.

Összehasonlítás alapú szelekció (SELECTION A <= v (R))

• Az eredményrekordok számának becslése: Ha v-t nem ismerjük, akkor n_r/2. Jobb hijján nincs jobb becslésünk, ettől van a legtávolabb a 2 worst case edge.
• Ha v-t ismerjük, egyenletes eloszlás esetén: n_átlagos = $$n_r\cdot \frac{v-\min (A,r)}{\max (A,r)-\min (A,r)}$$
• A6: Elsődleges index használatával, ha v-t nem ismerjük: E_A6 = HT_i + b_r/2 Átlagosan még blokkok/2 blokkot is megnézünk, ami nem kell.
  Ha v-t ismerjük: $$E_{A6}={\mathrm{HT}}_i+\lceil \frac{c}{fr}\rceil$$
• A7: Másodlagos index-es egyenlőtlenségi feltétel: E_A7 = HT_i +LB_i/2 + n_r/2 (utána index fának a levelein kell menni, ezek a levél blokkok rendezettek, a B* fának levél node-jait össze pointerezik, így ha tudjuk, hogy hány blokkot tudunk elérni, annyi lépésből el is tudjuk érni, ha elértük, akkor az ottani mutatókból átlagosan rekordszám fele kell. Össze-vissza vannak akármilyen blokkokban. Ez elég nagy becslés, átlagos esetben a blokkok száma fele helyett akár 50 db blokkot kell olvasni. Ekkor a folytonos adatfájlt lineáris kereséssel gyorsabban lehet olvasni. Ebben konkrétan az index feltétele lassítani fogja a rendszert, az erőltetett lineáris keresés miatt.)

Join

• Természetes illesztés
• Nested loop join, 2 for ciklussal, ha van illeszkedő érték akkor az eredményhez adjuk. Ez worst case b_r + b_s*n_r Az első a külső ciklus, + rekordok elérése a belsőben.
  Ha a memóriába belefér: b_r + b_s
• Block nested loop join: Ha tudjuk, hogy a blokkműveletek a kritikusak, akkor a blokkokat egy 4 for ciklussal tudjuk nézni, hogy ha találtunk egy illesztést, akkor nézzünk meg mégegyet. Már nem annyiszor kell végigpörgetni, ahány rekord van, hanem annyiszor ahány blokk van.
  b_r + b_r*b_s Ha van indexünk, akkor könnyebb, olvassuk a blokkokat és másik relációból már indexelten keresült. b_r + n_r * c_r. Ahol c helyére lehet index futást helyettesíteni.

További join implementációk

• Sorted merge join. Ez a legelterjedtebb, a 2 relációt rendezzük és csak egyszer végig kell menni.
• Hash join: Az illeszkedő rekordokat nem index, hanem hash táblán keresztül keressük.
• Bitmap index join.

Egyéb műveletek:

• Ismétlődés
• Projekció
• Unió
• ...

Kifejezésértékelések további módjai

• Materializáció: Meg kell várni, amíg egy kért query már előállt.
• Pipelining: Egymástól független query-ket előre vesszük, több modul dogozza ezeket fel. Ez nem mindíg alkalmazható.

Költségalapú optimalizációs implementációs

Fel kéne sorolni sok tervet és meg kell nézni mindegyikhez a becsült költséget. Amelyik a legalacsonyabb, azt választjuk.
Ez jól hangzik, de nem annyira működik.
A gyakorlatban az optimalizálók nem tudják a jó terveket (összeset) időben megtalálni. Ezt persze heurisztikákkal meg lehet találni.

Join algoritmusok

Ezeket tanuljuk a tárgy keretében. C++-ban újra implementálva:

SQL-re példák

Vegyünk egy repülőfoglalás rendszert, ezt mondjuk így ábrázoltuk: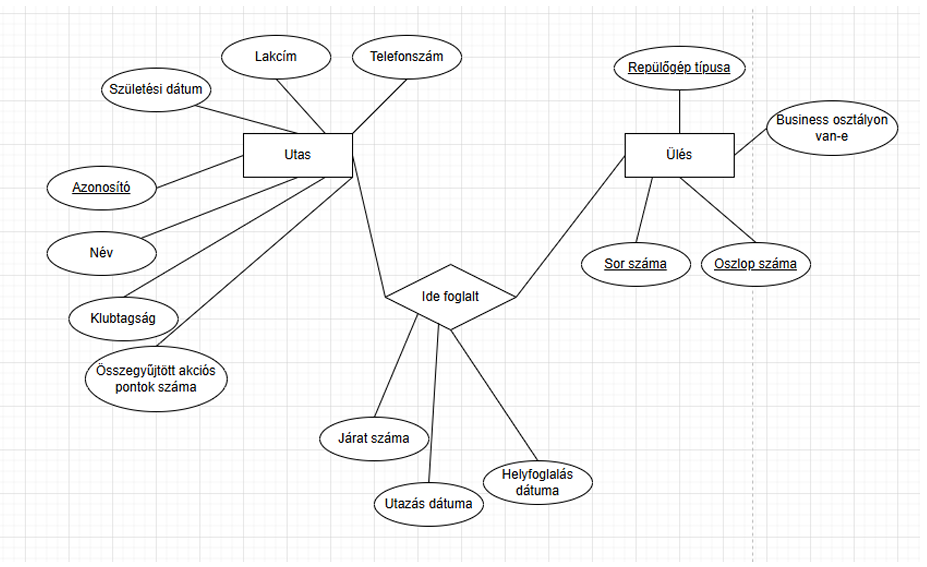
Ennek írjuk fel a sémáját gyakorlás képpen és adjunk egy mesterséges kulcsot ezekhez:

Utas(utas_id, azonosito, nev, lakcim, telefonszam, szul_datum, klubtagsag, akcios_pontok_szama)

Ide_foglalt(foglalas_id, jarat_szama, utazas_datuma, helyfoglalas_datuma, utas_id, ules_id(FK))

Ules(ules_id, sor, oszlop, repulogep_tipus, business_osztalyon_van_e)

Ha ezeket Oracle SQL-be táblákká akarunk alkítani, így tehetjük meg: CREATE TABLE Utas ( utas_id NUMBER CONSTRAINT pk_utas PRIMARY KEY, azonosito VARCHAR2(30) NOT NULL CONSTRAINT uk_utas_azonosito UNIQUE, nev VARCHAR2(100) NOT NULL, lakcim VARCHAR2(255) NOT NULL, telefonszam NUMBER(12), szul_datum DATE, klubtagsag VARCHAR2(10) NOT NULL, akcios_pontok_szama NUMBER(10) DEFAULT 1 NOT NULL, CONSTRAINT chk_utas_telszam CHECK (telefonszam IS NULL OR (telefonszam > 9999)), CONSTRAINT chk_utas_szul_datum CHECK (szul_datum IS NULL OR szul_datum > DATE '1910-01-01'), CONSTRAINT chk_utas_klubtagsag CHECK (klubtagsag IN ('SILVER', 'GOLD', 'PLATINUM')), CONSTRAINT chk_utas_akcios_pontok CHECK (akcios_pontok_szama >= 0) ); CREATE TABLE Ules ( ules_id NUMBER CONSTRAINT pk_ules PRIMARY KEY, repulogep_tipus VARCHAR2(50) NOT NULL, oszlop CHAR(1) NOT NULL, sor NUMBER(2) NOT NULL, business_osztalyon_van_e CHAR(1) DEFAULT 'N' CONSTRAINT chk_ules_business CHECK (business_osztalyon_van_e IN ('I', 'N')), CONSTRAINT chk_ules_oszlop CHECK (oszlop BETWEEN 'A' AND 'M'), CONSTRAINT chk_ules_sor CHECK (sor BETWEEN 1 AND 24), CONSTRAINT uk_ules_egyedi UNIQUE (sor, oszlop, repulogep_tipus) ); CREATE TABLE Ide_foglalt ( foglalas_id NUMBER CONSTRAINT pk_ide_foglalt PRIMARY KEY, jarat_szama NUMBER(10) NOT NULL, utazas_datuma DATE NOT NULL, helyfoglalas_datuma DATE, utas_id NUMBER NOT NULL, ules_id NUMBER NOT NULL, CONSTRAINT fk_foglalas_utas FOREIGN KEY (utas_id) REFERENCES UTAS(utas_id), CONSTRAINT fk_foglalas_ules FOREIGN KEY (ules_id) REFERENCES ULES(ules_id), CONSTRAINT chk_foglalas_datumok CHECK (helyfoglalas_datuma IS NULL OR helyfoglalas_datuma < utazas_datuma), CONSTRAINT uk_foglalas_egyedi UNIQUE (jarat_szama, utazas_datuma, ules_id) ); A logikát érdemes gyakorlásképpen átnézni.
A constraint-ok segítenek az értékeket megszorítani, hogy csak bizonyos értékeket lehessen felvenni a táblákba. Pl: Nem lehet illegális ülés sort vagy oszlopot felvenni.
Próbáljuk ezeket feltölteni értékekkel és nezzük meg, mit enged.

SQL clause magyarázatok

• SELECT: a projekciónak megfeleltethető.
• X FROM A: X oszlopot választja ki az A táblából.
• DROP TABLE táblanév: Kitörli a táblanevet
• CONSTRAINT név CHECK (kifejezés): A check kifejezés megfeleltet egy vagy több oszlopot, hogy a kifejezés igaz legyen, ha nem igaz, nem szerepelhetnek az értékek a táblába.
• PRIMARY KEY: Elsődleges kulcs
• FOREIGN KEY: Idegen kulcs
• INSERT: Új sort lehet beilleszteni egy táblába.
• UPDATE: Sor frissítésére alkalmas.
• DELETE: Sor törlésére alkalmas.
• WHERE: Szelekciónak megfeltethető.
• GROUP BY: Csoportosítja a kimenetet egy oszlop adatra. Excel szűrésnek megfeleltethető bizonyos szempontból.
• ORDER BY: ASC vagy DESC lehet. Vagy növekvő vagy csökkenő sorrend.
• HAVING: A group by-ra van. Csak azt adja a group by vissza, ami megfelel a having utáni vizsgálatnak.

Fizikai adatszervezés - feladatok

Ahhoz, hogy számolni tudjunk, szükségünk lesz mindenféle értékre előszőr. Ezeket az értékeket szoktuk használni és számolni:

• n_r: Rekordok száma,
• s_r: Rekord mérete, (size of record)
• k_r: Kulcs rekord mérete,
• p_r: A kulcs rekord pointerének mérete,
• B: Block capacity. Ez egy számérték, ami megmondja, hogy 1 blokk hány byte.

Adottak ezek az értékek:

• n_r = 1000
• s_r = 850 byte
• k_r = 50 byte
• p_r = 18 byte
• B = 4000 byte

Számoljuk itt ki a blocking factor-t! (F_r-t)!
Ez úgy számolható ki, hogy a blokk kapacitást elosztjuk azzal, hogy mekkora 1 blokk:
$F_r=\lfloor \frac{B}{s_r}\rfloor$
Azért vesszük az alsó egészrészét, mert 1 blokkon egész számú rekordot akarunk tárolni és 1 rekordot 1 blokkon akarunk csak tárolni. Szóval nem lehet az, hogy 1 rekord 2 blokkon is van. Pl: Ha a 3.4 rekord jön ki akkor 1 blokkon csak 3 egészet tudunk tárolni.
Behelyettesítve itt:
$F_r=\lfloor \frac{\mathrm{4000\; byte}}{{\mathrm{850\; byte}}_{}}\rfloor =\; 4$
Tehát ebben az esetben 1 blokkon 4 egész rekordot tudunk tárolni.
A következőt szeretnénk megtudni: Hány block lesz az index struktúra pointerekkel együtt?
Nos ahhoz, hogy ezt ki tudjuk számolni, meg kell határozni egy indexrekord méretét, ami egy kulcs + egy pointer:
$F_{\mathrm{r\_idx}}=p_r+k_r$
A mi értékeinket behelyettesítve ez:
$F_{\mathrm{r\_idx}}={\mathrm{18\; byte}}_{}+{\mathrm{50\; byte}}_{}={\mathrm{68\; byte}}_{}$
Hát ez remek, most a blocking factor képletet kell alkalmazni itt is, csak most nem egy adatrekord méretét használjuk, hanem az indexrekordét:
$F_r=\lceil \frac{\mathrm{4000\; byte}}{{\mathrm{68\; byte}}_{}}\rceil =\; 58$
Ha már tudjuk, hogy hány rekord van, akkor határozzuk meg azt is, hogy hány blokk van. Ezt ezzel a képlettel tudjuk kiszámolni:
${\mathrm{Blocks}}_{}=\lceil \frac{n_r}{f_r}\rceil$
Ebbe behelyettesítve azt kapjuk, hogy 1000/4 = 250. Azért kell itt most a felső egészrész, mert lehet, hogy annyi rekordunkra van, hogy szükségünk van még egy blokkra amit viszont nem használunk ki teljesen. Példa: Ha a blokkok 100 rekordot tartalmaznak, és nekünk 301 rekordunk van, akkor is 4 blokk kell, mert valahol azt az 1 rekordot is el kell tárolni, ami marad.
Mi a különbség, ha a blokk már a memóriába van eléréskor? Nos elég sok, mert nem kell betölteni.
Ha bináris kereséssel érünk el blokkot, akkor mennyi blokkművelet kell, ha 6 blokkunk van?:
$\lceil {\log }_2(1+6)\rceil =3$ Kell egy extra léptetés is, mert mi van, ha csak 1 blokkunk van és abba van az összes rekord.

(Vödrös hash átlag: láncolt listák hossza összeadva/B )

!!EDDÍG TART A ZÁRTHELYI ANYAGA!!

Visszatérünk a középső réteghez és egy alternatív logikai sématervezési opcióra fogunk ránézni.
Emélkeztető: Van a világunknak egy darabja. Ebből egy előmodellt állítottunk elő, ez pedig egy ER modell volt, aminek a grafikus reprezentációja az ER diagram.
Ebből az előmodellből állítottuk elő azt az adatmodellt, ami már alkalmas arra, hogy a világnak egy részének adatait leképezze és képesek legyünk annak a tudáshalmaznak amit leképezünk jól értelmezni, hogy ebből sok tudást tudjunk visszanyerni.
Ebből úgy lett adatmodell, hogy + művelethalmazt adtunk hozzá. Pl: Relációs séma.


Nem csak idegen kulcsokkal lehetne összedrótozni az adatokat, pl: pointerek, asszociációk.
Ezen az úton a világunk szemantikáját vittük bele, + formalizmusokat, model specific elemek.


Ez miért nem jó? Azért, mert nehéz észben tartani, hogy a relációs halmazokat egyes esetben hogyan kapcsoljuk össze. Ha ilyen módon tervezünk relációs adatbázisokat akkor anomáliák léphetnek fel.
Eddíg a kapcsolatokat inkább heurisztikusan állapítottuk meg, mint hogy az tudományosan lett volna megállapítva.
A tipikus műveletek ebben a környezetben: update-insert-delete műveletek a lehető leghatékonyabban legyen végrehajtható.
Ennek függvényében megkülönböztetünk update-insert-delete-anomáliákat:
Konkrét példa adatbázis: Szállító: Egy adott boltba mindenféle termékeket szállítanak be, ennek vann neve, címe, terméknév, ár. Ilyen adatok vannak azb adatbázisban: Kis a János utca 1.-ben tejet szállít 2FT-ért.

Név	Ide szállít	Mit szállít?	Mennyiért?	Lakik?
János	Ló utca 1.	Tej	2 FT	Ló utca 1.
János	Ló utca 2.	Vaj	2 FT	Ló utca 1.
Tamás	Ló utca 1.	Tej	3 FT	Ló utca 1.

No, itt mi történik, ha János lakcímet vált. Logikus lenne, hogy minden rekordba átírjuk, de baromi lassú lenne. Ha pl: Kevés Tamás rekord van, akkor ha Tamás költözik, akkor a válaszidő kevesebb, míg ha Jánosnak több rekordja van akkor a válaszidő több. Ez a rendszer válaszidő szempontjából tervezhetetlen.
Ez az egyik update anomália.

Nézzünk példát a beszúrásra: Tamás új dolgot is akar beszállítani, amihez új rekord kell.
Hogyan lehet új rekordot felvenni? Úgy, ha ki tudjuk tölteni az új rekordot adatokkal. Tipikusan valami kézi adatbevitellel szokták csinálni. Be kell gépelni a címet, nevet, ilyesmit... Ez azért baj, mert ha elgépeli a címet akkor baj van, vagy az is lehet, hogy már a cím frissült.
Előfordulhat, hogy cím helyére nem a kívánt adat került. Lehet erre minden ellenőrzést írni, működik de ez + gépidő az optimális adatszervezésel szemben.
Akkor már miért nem 1 helyen tároljuk a címet? Pointerezzünk! Ez volt az insert anomália. A másik probléma akkor merül fel, ha új szállítót veszünk fel.
Benedek szeretne beszállítani, még nem szállított be semmit, de fel kell venni az adatbázisba. No, most ebbe a rekordba a Név+Termék egyedileg meghatározza a rekordokat
Na, most ez az összetett kulcs nem áll ilyenkor rendelkezésre, lehet rakni NULL értéket, de akkor már nem kulcs a kulcs. Látszik, hogy a megoldás ebben az esetben nem triviális
Ez volt a 2. insert anomália
Törlési anomália: Egy szállító mert nem szállít egy bizonyos terméket. Ilyenkor törölni kell egy kulcs EGY RÉSZÉT. Ez baj, ilyenkor csak azt tudjuk csinálni, hogy töröljük a sort. Igen, de mi van, ha az a beszállító utolsó terméke volt? EKkor már a beszállító neve NEM lesz benne az adatbázisban. Rosszul van tárolva. Mi van, ha akarom tudni, hogy kinek számlázzak? Nem tudok, mert lehet, hogy nincs benne már a beszállító neve.
Redundancia: Akkor van, ha egy adatot többször tároljuk el attól még nem redundancia, csak akkor redundancia, ha az értékismétlődés felseleges. Pl: Név helyett beszállító id a táblában. Így egy helyen van a név. Egy adatbázis redundáns akkor, ha valamely benne lévő attribútum értékét ki lehet következtetni valamely másik attributum értékéből valamilyen ismert következtetési szabály felhasználásával. Reláció redundancia: Egy reláció redundáns akkor, ha benne lévő valamely attributum értékét ki lehetne következtetni egy másik attributum értékével egy jól definiált megkövetkeztetési szabály alapján. Ha ezt a redundanciát megszüntetnénk, akkor az insert-update-delete műveletek hatékonyabban lehetnének végrehajtva. Hogy lehetne? Úgy, hogy specifikus kényszereket építünk be a tervezési folyamatba.
Pl: Nem lehet string idegen kulcs. Hülye, egyszerű kényszer.

Kényszerek

2 féle van, érték függő és független.
Értékfüggő kényszer: Olyan kényszer, ahol egy mező értékét korlátozzuk egy intervallumba vagy konkrét értékekre. Pl: 30-tól nagyobb emberek testmagassága nem lehet kisebb, mint 20 centi. Értékfüggetlen kényszer: Olyan kényszer, ami nem függ konkrét értéktől. Pl: Tartalmazási függés: Van egy vállalat, vannak dolgozók és osztályok. Vannak kulcsai mindkettőnek, az, hogy ki hol dolgozik leírható úgy, hogy egy másik táblába összerendeljük a 2 idegen kulcsot, ez lesz az "Itt dolgozik" tábla vagy reláció. Ebben csak olyan id-k jelenhetnek meg, amik a másik táblákba is benne vannak. Ha olyan jelenne meg, ami nincs benne a dolgozó ba, akkor az ilyen fantom dolgozó lenne. Lehet még funkcionális függés: Kiváló példa az, hogy a név és cím között 1:1 kapcsolat van. "1 db szállítónak csak 1 címe llehet". Tudhatjuk, hogy ahol felbukkan a szállító neve, ott a címnek is ugyanannak kell lennie.
"A név meghatározza a címet"
Pl: Egy ember személyi száma meghatározza az ember nevét, címét, születési dátumát, stb.
Most a világunkat elsődlegesen funkcionális kényszerekkel fogjuk képezni. Egy függés modelt alkotunk. A függés model az ugyanúgy az adatszemantikát fogja az adatmodellbe behozni.
Pl: NÉV meghatározza: CÍM. Ha ez az értelmezés olyan, hogy legfeljebb 1 cím tartozik 1 névhez, akkor már tudjuk mondani, hogy a névtől függ a cím.
Ekkor az ember (Név, Cím) helyes lesz. Ekkor mondjuk más struktúrákba is be lehet írni a nevet Beszállít(Áru_id,Név,ár,hova)
Ilyenkor már nem írjuk ki a címet redundánsan többször.
Legyen a táblának 2 sora, X és Y. És ebben az attríbútumhalmaz értéke x és Y-ban x'. Ha ezek a 2 sorban megegyeznek ezek az x-ek és egy y másik attributum szerint is megegyeznek, valamint stimmel rájuk a séme akkor tulajdonképpen formálisan az lett kijelentve: A szállító neve és címe között akkor van funkcionális függőségi viszony, ha a név értékkor csatlakozásnál a cím is az.
Ez így jó-e. Nem, mert egy adott reláción nem feltétlen teljesül a szemantikus adatfüggés. Adatváltozáskor nincs ez betartatva.
Itt azt formalizáltuk, hogy X és Y attributumok között mikor áll fel a funkcionális függőség?
- 2 Sorban az X értékek megegyeznek. (P= 2 érték megegyezik)
- 2 Sorban az Y értékek megegyeznek. (Q= megegyezhet valami vagy nem egyezhet meg, tökmindegy)
Kapcsolótáblánál 2 kulcs kell.
Implikáció 2: 2 változós logikai függvény. Ha A implikálja B-t: Ha A=B=1, akkor igaz, akkor is igaz, ha A igaz, másképp hamis. (Igaz, ha A = 1 vagy 0 és B = 1) A következtetési szabály a redundanciához: Fennáll-e a funkcionális függőség?
Ez alapján következtessük ki a címértéket. Ha mondjuk az egyik sorban ki töröljük a címet DE mi egy másik adat / információ alapján ki tudjuk következtetni, hogy ott mi állt akkor az ott redundáns érték volt.
A funkcionális függőség fennáll, ha a névértékek megegyeznek és a címértékek megegyeznek.
Ekkor a cím értékét ki tudjuk következtetni, mert P értéke 1.

Funkcionális függések alapján fogalmak újradefiniálása

Jelölés: A,B,C attríbútumokat, X,Y,Z adott halmazt, R,S,T -val egy adott sémát. Determináns: Legyen egy relációs sémán egy X és Y halmaz és teljesüljön az a feltétel, hogy az X meghatározza Y-t, ekkor X Y determinánsa. (Ha teljesül az, hogy ha az X meghatároz egy olyan halmazt ami megegyezik a teljes sémával (OMEGA)). Kulcs 2: Ha X meghatározza OMEGA-t és nem létezik x' részhalmaz ami minimum meghatározza az OMEGAT-t akkor az X neve: kulcs. Itt az egyediséget már megkívánjuk. Szuperkulcs: Arról beszélünk, ha X meghatározza az OMEGA-t. Nincs minimalitási feltétel. Részleges és teljes függés: ha X meghatározza az Y-t és létezik olyan x' részhalmaz ami meghatározza az Y-t akkor Y részlegesen függ X-től. Ha nincs ilyen x' akkor van teljes függés. Egyszerű / összetett kulcs: Ha egy kulcsnak csak 1 attribútuma van akkor egyszerű, másképp összetett / kompozit. Ha kulcs akkor minimális, ha nem minimális akkor szuperkulcs. Idegen kulcs: Ha X kulcs akkor x' OMEGA-ban idegen kulcs, ha x' X-ben kulcs Név: Ha x1,x2,xn OMEGA kulcsai akkor ezek közül az egyiket döntés szerint elsődleges kulcs lesz. A többi neve pedig kulcsjelölt lesz. Omega halmaz és kulcs közötti kapcsolat: Ha a séma kulcsai x1,x2,xn akkor az uniója az xi halmazoknak fogja megadni az elsődleges attributumok halmazát. Az OMEGA - Elsődlege attributumok = Másodlagos attributumok. Tétel: Minden relációs sémára létezik legalább 1 kulcsa.

Relációs sématervezés normalizálása (Ismétlés)

Probléma: Egy megoldásra / specifikációra több, különböző ER diagram létezik. De melyik a legjobb?
Meg kell fogalmazni, hogy milyen értelemben a legjobb?
Cél: Az olvasásokat a legnagyobb hatékonysággal és biztonsággal lehessen olvasni / írni.
Legyen egy olyan reláció ahol szállítóknak az adatait tároljuk:

Név	Cím	Tétel	Ár
Ferenc József	Ló utca 1	Víz	10 FT
Jani	Ló utca 2	Víz	10 FT
Ferenc József	Ló utca 1	Tej	20 FT

Ami szembetűnő, hogy a nevek, címek, tételek és árak ismétlődnek. Ez nem jó, többször kell eltárolni, de vannak más bajok is.
Teljesen redundáns a név melett a cím, mert már a névből kiderül, hogy hol lakik az ember.
A szállítót sem kellene annyiszor azonosítani, ahány terméket szállít.
Az is érdekes, hogy hogyan korrelál az áru név az árával.

Redundancia

Sok fejtörést fog okozni.
Insert, Update, Delete anomáliákat fog előidézni.

Update anomália

Akkor találkozunk ezzel, ha Ferenc József elköltözik, mert ekkor nem hatékonyan, sokkal többször kell átírni ugyanazt az információt. Ez itt nem baj, de mi van, ha ő 1000000 terméket szállít. Akkor már lassú lesz az update NAGYON.
Az is lehet, hogy Ferenc József rekordjai külön blokkokban vannak, nem tudjuk, hogy mennyi blokkművelet lesz ez.
A legsúlyosabb az, hogy ha több rekordba is van ez a cím akkor nincs felső korlát amit mondani tudunk hogy mennyi rekordot kell átírni. Ekkor időt se tudunk mondani.

Insert anomália

Egy új rekordot szeretnénk Janinak bevinni mert már téglát is szállít. Ekkor be kell vinnünk a nevét + címét de véletlen régi címet viszünk be. Ekkor a jó cím információ elveszhet, mert manuálisan kell azt bevinni.
(Lásd: Gizi néni az MNB-nél szar email címet visz fel az adatbázisba)

Delete anomália

Ha én egy tételt ki akarok törölni akkor egy sort ki kell törölnöm. De ha kitörlöm Jani tételét, akkor maga a beszállító adata is megszűnik azzal, hogy 1 tételt ki töröltünk.

Megoldások ezekre

A relációinkat az univerzális relációból egyre kisebb, több relációra fogunk bontani úgy, hogy ezek az anomáliák nem forduljanak elő.
Pl:

Név	Cím
Ferenc József	Ló utca 1
Jani	Ló utca 2
Ferenc József	Ló utca 1

Név	Tétel	Ár
Ferenc József	Víz	10 FT
Jani	Víz	10 FT
Ferenc József	Tej	20 FT

Érezhető, hogy ezek a táblák ugyanazt az infót hordozzák de már az anomáliák nélkül.

Funkcionális függés

Példa: Név meghatározza a Cím-et. NÉV->CÍM
Érdemi függés: FOR ALL t, t' ELEMENT OF r(R), t[X] = t'[X] esetén A attributumra t[A] = t'[A].
Fontos, hogy ezt egy ha-akkor állítással lehet modellezni, de ez implikáció, szóval a ha-tól függetlenül igaz lesz a "q akkor", csak akkor nem ha a "p ha" igaz.
Pl: Egy egy sorú sémába minden funkcionális függőség teljesülni fog. (Gondoljunk bele, a szuper kulcs mindent is meg fog határozni ahhoz az 1 sorhoz).

Normál formák

Ezek tulajdonságok gyűjteményei, ami arról szól, hogy ha egy adott séma egy formára illeszkedik akkor a séma redundancia jellegére jellemezhető lesz.
1NF: Egy relációs séma első normál formában lesz akkor ha a sémában valamennyi attribútum atomi. Pl: Az attribútum akkor atomi, ha egy attribútum-ot nem bontunk szét több elemmé és azokon nem végzünk több külön műveletet. Pl: Az életkor legyen csak életkor és ne tárolja pl: az első 2 bitje az ember nemét IS. Ez példáúl nem teljesíti az 1NF-et:

Osztály	Cég	Dolgozók
Marketing	Valami KFT	Matyi, Jani, Feri, Juli

Ezt 0NF-ről 1NF-re így lehet átírni:

Osztály	Cég
Marketing	Valami KFT

Név	CégID	Dolgozók
Matyi	Valami KFT
Jani	Valami KFT
Feri	Valami KFT
Juli	Valami KFT

Fontos, hogy ez még nem segített a redundanciába, majd a 2NF és felette lesz. 2NF: Akkor van egy relációs séma 2. normálformában ha már 1NF és minden másodlagos attribútuma minden kulcstól teljesen függ. Vagyis, nem található mondjuk olyan ahol 2 kulcs van de mégis 1 kulcscsal is meg tudunk határozni az attribútumot. 2NF-nél nem szabad, hogy bármely kulcs akár csak a részhalmaza is determináló legyen. (Pl: A nevek, mint "Szabó Ferenc" egy része meghatározó is lehet, ez már szélsőséges de ezért kell mesterséges kulcsokat használni).
Pl: R(A,B,C,D) F = {AB -> C, B->D} ekkor, AB szuperkulcs. Próbáljuk elvenni az A-t, B meghatározza magát + D-t, A meg csak magát. Ekkor nem tudunk részt elvenni és minimális is szóval kulcs.
Az A és B elsődleges míg a C és D másodlagos, viszont a kulcs valódi részhalmazától függ a D (B-től), ez sérti a 2NF-et. Tehát ez csak 1NF.
Pl: Ha több rekordnak is b1 a B attributuma akkor az azt implikálja, hogy több ugyanolyan D lesz, ami probléma a redundancia miatt. Ekkor ezt meg kell szüntetni.
Ha egy relációs sémának minden kulcsa egszerű kulcs akkor az mindíg 2NF lesz.
Bizonyítás: Belátható, hogy a kulcsoknak nincs részhalmaza ami determinál tehát a 2NF teljesül.
Tranzitív funkcionális függőség: Van X egy részhalmaza az univerzumnak és Y és A attributuma és X meghatározza Y-t és Y meghatározza A-t és A != Y, akkor A az X attributum halmaztól tranzitívan függ. Ez akkor van, ha van egy attributum halmaz, ami az Y értékekekt meghatározza, ami pedig A-t meghatározza. Tehát X meghatározza A-t indirekten. 3NF: Egy séma akkor 3NF akkor ha 1NF és egyik másodlagos attributum sem függ tranzitívan a kulcstól. 2. Definició: 3NF: A séma 1NF FOR ALL X → B | B != X esetén X szuperkulcs vagy B elsődleges attributum. Tétel: 1. Def = 2. Def.
Bizonyítás: Tegyük fel, hogy nem szuperkulcs / elsődleges attributum-ra is igaz lenne az 1. def. Ekkor azt állítjuk, hogy függhet tranzitívan egy 2.-lagos attributumtól egy másik másodlagos attribútum. Pl: Foglalások vannak termekre, melyeknek az ID-jét, a teremkódját és a terem max létszámát tároljuk. Egy sor lehet pl: (1|E1A|300) A foglalás id a kulcs, amitól függ a terem szám másodlagos attributum viszont a teremszám meghatározza a létszámot. Ekkor a 2. def-t sértené + magát is.
BCNF: 1NF és attributum nem függ tranzitívan kulcstól. 2. Definició: BCNF: A séma 1NF FOR ALL X → B | B != X esetén X szuperkulcs alternatíva nélkül. Tétel: 1. Def = 2. Def. és a BCNF resztriktívebb, mint a 3NF.
Bizonyítás: Triviális belátni, hogy a definicióból jön a resztriktívebb természet. a BCNF megkívánja, hogy FOR ALL X → B X-nek szuperkulcsnak kell lennie, a 3NF viszont megengedőbb, mert elsődleges attributum is lehet.
Tétel: BCNF > 3NF > 2NF > 1NF (erősség szempontjából).
Bizonyítás: Az BCNF > 3NF beláttuk feljebb. Az is triviális, hogy 3NF,2NF > 1NF, mert az 1NF feltétele a 2 és 3NF-nek.
Tétel: A BCNF funkcionális függőség redundanciamentes.
Bizonyítás: A redundancia egy Z → B nemtriviális funkcionális függőségtől lesz, ahol Z nem szuperkulcs, ismétlődés miatt, (azért okoz redundanciát, mert 2 ugyanolyan Z-hez (mivel nem szuperkulcs, lehet és értelmes) 2 ugyanolyan értéket rendelünk B-re) ezért egy 2. attributumot kötelező jelleggel kellett meghatározni. A BCNF definíciója szerint minden Z → B függésre Z-nek szuperkulcsnak kell lennie. Ekkor ha a Z szuperkulcs, akkor nem ismétlődhet és B-t se lehet kikövetkeztetni (redundánsan). Ellentmondás. Így nincs redundancia.
Tétel: 3NF(R) → 2NF(R).
Bizonyítás: TFH. hogy R nem 2NF de 3NF. Ha nem 2NF akkor EXISTS k'→B ahol k' egy kulcs része, akkor B részlegesen függ k-tól. Ekkor nem teljesül a 3NF, ami szerint FOR ALL X → B | B != X esetén X szuperkulcs vagy B elsődleges attributum. Egyik se teljesül, tehát ellentmondásba jutottunk.
Cél: BCNF-sémák konstruktálása lesz.
Egy függőség lehet eseti, amikor 1 sémán áll fenn és érdemiek, amik több sémán vannak.
Az érdeminek van ismert (mert adott vagy modelleztünk) és nem ismert (viszont létezhet) is van.
A célunk ezeknek a függésegnek a kiderítése.
Tervezzünk egy mechanizmust ami inputnak kap már meglévő funkcionális függőséget és azokból kiad új funkcionális függőségeket. El kell várnunk, hogy értelmes függéseket adjon ki, legyenek azok helyesek. A 2. elvárás pedig az, hogy ha egy függéshalmaz mellett végez inputból az összeset állítsa elő az össze függést. Nem hátrány, hogy a fekete doboz egyszerűen működik + hatékony.
Igaz függés: Egy adott A funkcionális függéshalmaz meg van adva és A → Y (Y is funkcionális függés halmaz) akkor ha egy reláción A teljesül akkor Y is teljesüljön. Ezt elég nehéz lesz megcsinálni. Kellenek szabályok amik véges számú alkalmazásával új helyes függőségeket kapunk.

Armstrong axiómák

3 db szabály:

• Ha Y részhalmaza X-nek akkor X → Y (triviális funkcionális függőség)
• Ha X → Y-t és Z attributummal kibővítjük mind kettő sémát akkor XZ → YZ
• Ha X → Y és Y → Z akkor tranzitívan X → Z-t.

Tétel: Ha egy szabály sorozata segítségével le lehet a függést vezetni akkor ezekkel levezetett függőség mindíg helyes lesz. (Igazság tétel)
Bizonyítás: Meg kell mutatni, hogy mind a 3 axióma magában igaz. Reflexivitás helyessége: def. szerint igaz, Bővítés helyessége: logikailag megőrző lépés, Tranzitivitás helyessége: implikáció + "ha-akkor" logika alapelve. Ha minden axióma helyes és csak helyes állításokat lehet helyesből levezetni akkor minden fasza.
Tétel: Ha van egy funkcionális függőség F mellett ami helyes akkor ezt a függést le is lehet vezetni a 3 szabállyal. (Teljességi tétel)
Bizonyítás: Megmutatható, hogy az Armstrong axiómak az attribútumzárás eredményhalmazát adják (ami ugye azokat használja). X legyen az attributum halmaz és X+ a lezártja. ekkor FOR ALL Y ELEMENT OF X+-ra igaz, hogy X→Y-t, ahol F függőség mellett az igaz.
Állítás: Minden funkcionális függőség helyes ami levezethető és ami helyes az levezethető.
Ez nem oldja meg minden problémát, Pl: Z → T függ? Ha T helyes akkor véges időn belül megkapjuk. De mi van ha T nem helyes? Akkor véges lépésből nem jön ki.
Cél: Próbáljuk meg a teljes helyes halmazt előállítani. Ennek a halmaznak az ismeretével jobban tudunk erre válaszolni.
Zárt függés halmaz: Teljes, helyes véges halmaz ami F-szabályokból levezethető függések. Ekkor megmondhatjuk, hogy mi helyes, azaz mi van benne ebbe a halmazba.
Gyakorlatba ez bajos, mert B1 B2... Bn függés az A-n 2^n db részhalmaza lesz. Ekkor exponenciális lesz a feladat.
Attributum halmaz lezártja: Teljes, olyan halmaz amire igaz, hogy F (X → A)-t akkor van benne az A. Akkor ez a halmaz F szerinti lezárt. Ezt a lezártat egy rekurzív algoritmussal lehet kiszámítani. X legyen a halmaz, ekkor minden iterációba veszünk be olyan attributumokat amelyek Z-k és Z legyen részhalmaza Xi-nek (i = tetszőleges X indexe). És Z → T ELEMENT OF F és A ELEMENT OF T.
Ez közel-lineáris időben meg mondja a függéseket, vagyis a halmazt amiből a függéseket meg lehet állapítani majd.
Példa az algoritmus futárára:
Legyen R(ABCD) és X= AB (Meghatározzák a séma összes attributumat) X(+) = ?
X(0) = AB
X(1) = AB UNION {C}
X(2) = ABC UNION {D}
X(2) = ABCD
Ekkor AB szuperkulcs.

Tranzakciókezelés

Eddíg olyan adatbáziskezelőbe gondolkoztunk aminek volt 1 usere, 1 CPU-ja és 1 háttértára.
Hát ez nem túl attraktív, de ez az alap.
De mi van, ha a feladat az, hogy több felhasználót is ki tudjuk szolgálni.
Ilyenkor ezek merülnek fel:

• Mi van, ha nem elég gyors?
• Mi van, ha nem elég védett?
• Mi van, ha nem elég hatékony?
• Mi van, ha nem elég robosztus? (hibatűrő)

Ezekre külön-külön szép megoldásokat lehet adni. Pl: Gyorsaságra: párhuzamosítás, védettség: elosztott DBMS, redundancia, védett: új security módszerek, robosztus: jobb, finomabb algoritmusok, több felhasználó: konkurens működés.

Konkurens működések

Tranzakció: Egy program egyszeri végigfutása ami vagy hibátlanul lefut vagy semmilyen hatása nincs. Ezek egyidejűleg szoktak futni vagy több CPU-val vagy időosztásos módszerben.
A probléma ott kezdődik, hogy idő előtt befejeződhetnek + összefésülődhetnek.
Előfordulhat, hogy a futtató szándékosan ki fogja lőni a tranzakciót.
A problémának 4 alapesete van.

Elveszet módosítás (Lost update)

Ütemezés: T1,T2...,Tn tranzakció időbeli akcióit futtatja. Példa:

Lépés	T1 művelete	T2 művelete	Megjegyzés
1	R(X) → X = 100		T1 beolvassa X értékét (100)
2		R(X) → X = 100	T2 is beolvassa a régi X értéket
3	X = X + 50 → 150		T1 módosítja magában az értéket
4		X = X - 30 → 70	T2 is módosítja a régi értéket
5	W(X) → 150		T1 kiírja X = 150-et az adatbázisba
6		W(X) → 70	T2 felülírja T1 frissítését → **Lost Update**

Nem megismételhető olvasás (Non repeatable read)

Példa:

Lépés	T1 művelete	T2 művelete	Megjegyzés
1	R(X) → 100		T1 elolvassa X eredeti értékét (100)
2		W(X) → 130	T2 módosítja X értékét 130-ra
3	R(X) → 130		T1 újra olvas → más értéket kap! (Nem megismételhető olvasás)

Az olvasások nem ugyanazt az értéket adják.

Fantom olvasás (Phantom read)

Példa: T1 Egy adott SELECT-et hajt végre és egy adott rekordhoz ér hozzá.
T2 Ezek után T2 INSERT-et hajt végre.
Ekkor itt a select ismétléskor már mást ad vissza.
Hasonló, mint az előző, csak ez nem tetten érhető mert T2 még nem feltétlenül fejeződött be.

Piszkos adat olvasása (Dirty data read)

Példa:

Lépés	T1 művelete	T2 művelete	Megjegyzés
1	BEGIN		T1 tranzakció indul
2	W(X) → 200		T1 módosítja X-et 200-ra (még NINCS commit)
3		R(X) → 200	T2 elolvassa T1 nem commitált értékét → **piszkos adat**
4	ABORT		T1 irregulárisan abortál → az X=200 SOSEM szabadott volna látszódni
5		→ T2 hibásan számol tovább a piszkos értékkel	A rendszer állapota inkonzisztens → Dirty Read anomália

Piszkos adat: Az az adat, amit olyan tranzakciók állítottak elő, amik nem regulárisan terminálódtak.

Minimum elvárások a DBMS-el

ACID: Követelmények: Atomicity (Atomiság: Vagy végigfut a tranzakció vagy semmi nem történik), Consistency (Konzisztencia: Ellentmondásmentesség olyan értelemben, hogy ha egyszer a programozó definiál tranzakciókat, akkor a DBMS biztosítsa hogy azok közül csak a sikeres tranzakciók eredményeit futtassa), Isolation (Izoláció: A DBMS-ben fussanak úgy a tranzakciók, hogy ne lássák a többi tranzakciót), Durability (Tartósság: Ha a DBMS végrehajtott egy tranzakciót akkor annak az eredménye ne veszhessen el)

Zárak használata

Zár: Hozzáférési privilégium ami adható és visszavonható. Egyszerű zár: Ha egy ilyen zárat egy adategységen elhelyezünk, akkor ahhoz csak egyszerre 1 tranzakció fér. Ilyenkor a többi várakozik.
Ez a Lost read-et kiküszöböli. Példa: 1 LOCK(X) T1 zárolja X-et → más tranzakció nem írhat/olvashat 2 R(X) → 100 T1 beolvassa X eredeti értékét 3 X = X + 50 → 150 T1 elvégzi a módosítást 4 W(X) → 150 T1 kiírja a friss értéket 5 UNLOCK(X) T1 feloldja a zárolást 6 LOCK(X) T2 most már lefoglalhatja X-et 7 R(X) → 150 T2 már a friss értéket olvassa 8 X = X - 30 → 120 T2 módosítja az aktuális értéket 9 W(X) → 120 T2 kiírja az értéket 10 UNLOCK(X) Zárolás felszabadul A lost read nem veszhet el, mert a T2 nem is tud hozzányúlni amíg az adatot T1 lockolta.
Várakozás: Ha Tm egy olyan adatot szeretne módosítani amit Tn tranzakció már lezárt akkor Tm várakozik amíg Tn unlock-ol.

Tranzakciókezelés - több felhasználók

Az ACID betartására vannak algoritmusok, protokollok, de nem minden algoritmus old meg minden problémát. Van, ami csak 1-et, más 2-t biztosít.

Zárak problémái

• Éhezés
• Live lock
• Patthelyzet (Deadlock)

Legális ütemezés: Akkor legális, ha egy tranzakció várakozik akkor ha olyan adatot akar zárolni, amit egy másik tranzakció már zárolt és az összes zárját felszabadítja a futása vége előtt. Ha egy ütemezés az sorosítható és bejön egy él ami miatt már nem lesz DAG, akkor a T1 várakozásra kényszerül.
2 Fázisú zárolás: Egy 2 fázisú zár protokoljait követő protokolt tartó ütemezés (legális) sorosítható, ha 2 fázisú.
Zárpont: Egy időpillanat a 2 fázisú zárprotokol életében ahol már az összes zárt megkapta. Időben a zárpontokat lehet vizualizálni. Ha növekvő sorrendbe rakja az ember a zárpontokat, akkor kijelenthető, hogy a zárpontok időben növő sorrendje soros ekvivalens.
Az Oracle-be 200+ zár is található. Különböző zárak lesznek hatékonyak egy-egy példára.
Read/Write lock: Olvasást vagy írást zár.

Zármenedzser

Van egy zártáblánk, ami egy zármenedzsernek dolgozik, mely egy ütemezővel dolgozik együtt.
Ilyen sorok vannak a zártáblában: Adategység|Zárak: Z1,Z2...Zn
Az ütemező dönti el, hogy egy beérkező tranzakcióval mi legyen. Pl: Várakoztathatja, jóváhagyhatja vagy egy másik T-t kilőhet a hatására.
Lehet az, hogy egy tranzakció már rég el akarja érni az adatot de ha nincs FIFO akkor éhezés lesz.

Holtpontok elleni védekezés

Egy T tranzakció lokkoljon le mindent amit használni fog indulásakor.

VAGY

Sorrendet felállítani a tranzakciók között.
Várakozási gráf: Irányított gráf, csomópontok tranzakciók Ti és Tj között akkor lesz előre él ha Ti várakoztatja Tj-t. Ez akkor van, ha Ti már zárolta azt, ami Tj-nek kell. Tétel: Adott pillanatban nincs patt, pontosan akkor ha a várakozási gráf DAG. (Irányított kör mentes).
Bizonyítás: 2 irányba kell: Nincs patt -> DAG: Tegyük fel, hogy igaz, akkor nem DAG, ami hülyeség. TFH. van irányított kör, ekkor a tranzakciók Ti és Tj egymást várakoztatják tehát patt van -> nem igaz szóval a tétel igaz. A gráf csomópontjait lehet topológikusan rendezni, akkor az DAG és van egy olyan csomópont, amiben él nem mehet, ennek törlésével újra ilyen pontok lesznek, ezt N-szer ismételve beláthatjuk, hogy nincs patt.

Ütemezések jellemzése

Egy ütemezés csak akkor pattmentes ha a várakozási gráfja DAG.
Egy ütemezés sorsítható: Ha a tranzakciók nem tudják átlapolódással befolyásolni egymást. De kell egy algoritmus ami a gyakorlatba el tudja dönteni, hogy valami sorosítható-e. Mi van, ha több 1000 tranzakció fut? A gráf nagy lesz. Ha sok közös adatot használnak akkor sok él lesz.
Soros ekvivalens: Egy olyan ütemezési sorrend, ami lefut pattmentesen. Ekkor sorosítható egy ütemezés, ha van soros ekvivalense.
Ha nem sorosítható, akkor a végeredmények függenek a sorrendtől -> RACE CONDITION

Izolációs elv

Akkor fogadjuk el az ütemezés eredményét ha olyan eredményt ad, mint amikor a tranzakciók úgy futottak le, mint ha egyedül csak azok futottak volna.
Valahogy el kell dönteni egy ütemezésről, hogy sorosítható vagy nem.
Ha egy ütemezésről kiderül, hogy sorosítható, és mi nem sorosíthatóként kezeljük az nem akkora hiba, mint fordítva.
Ennek megállapítására feltételezzünk egyszerű tranzakció modellt:
1 Adategységen csak 1 zár lehet 1 időben.
Sorosítási gráf: Pontosan akkor sorsítható az ütemezésünk ha a sorosítási gráfja (precedencia gráfja) az DAG. Ez a gráf az, hogy T tranzakciók a node-ok és előreélek a függőségek. Ha Ti használta A adatot és elengedte, majd Tj is A-t használja, akkor Ti->Tj-be egy irányított él kerül be. Ezzel azt akarjuk kifejezni, hogy minden soros ekvivalensben Ti-nek korábban kell lefutnia, mint Tj-nek.
Ha egy tranzakció egy adategységen zárat helyezett el, akkor írhatta és olvashatta.
Így viszont Tj akciói függ Ti-től.
Ekkor BÁRMELY soros ekvivalensben Ti-nek kell lefutnia. Ezért kell a nyíl Ti->Tj.

Minden műveletkérés után meg kell nézni, hogy megengedjük-e az új tranzakciót. Minden egyes adatmódosítás és zárkérés között meg kell nézni a sorosíthatóságot.
Egy tranzakciót abortálni kell, ha kört okoz elő a sorosítási gráfban. Akkor lesznek bajok, ha egy olyat lövünk ki, ami már adatot írt.
A körök keresése viszont drága, inkább check helyett kényszerítsük ki, hogy nem is lehet nem DAG a gráf: A protokollok fognak segíteni.

2 Fázisú zár (2 Phase Lock)

2 Fázisú zár: Egy T tranzakció zárat elengedni csak azután lehet, ha a tranzakció már az összes zárját megkapta. Egyszerű protokol, künnyű betartani.
Tétel: A 2 fázisú protokolt betartó tranzakció ha legálisak akkor sorosíthatóak.
2 Fázis: Zárak növekedése, egyre több zár, 2.: Az összes zár meg lett kapva, innentől csak csökkennek a zárak.
Zárpont: Az a pont, amikor a tranzakció az öszes zárát megkapta. Tétel: Ha zárpontokat egy időben növekvő sorrendje az adott ütemezésnek egy soros ekvivalense lesz.
Tétel: Egy DAG topológikus rendezése mindíg soros ekvivalens lesz.

RLOCK-WLOCK model

RLOCK: Egy puha, megosztható zár, ebből több tranzakció is el tud helyezni egy adaton többet. WLOCK: Egy kemény, nem megosztható zár, ebből egy tranzakció tud csak elhelyezni egy adaton. Miért jó ez? Azért mert ekkor a sorosítási gráf kisebb eséllyel fog irányított kört tartalmazni.

1. Ti vagy egy RLOCK vagy WLOCK utána UNLOCK, ezután Tj WLOCK. Ekkor Ti->Tj.
2. Ti vagy egy WLOCK utána UNLOCK, ezután Tj RLOCK. Ekkor Ti->Tj.
3. Ti vagy egy RLOCK utána UNLOCK, ezután Tj RLOCK. Ekkor teljesen mindegy, mert read after read van, az adat értékét 1 tranzakció sem módosítja, nem kell semmilyen él.

Ekkor az ütemezések nagyobb valószínűséggel sorosíthatóak.
(Az oracle-ben 200+ zár van)

Az adategységek hierarchikus viszonyban vannak

Ekkor baj van, logikusan ha egy adatot lockolnak, akkor ami alá tartozik azt is lockolni kell. (Ez intuíció).
Hierarchikus adategységek:

• Hierarchikus adatmodell
• B* fa
• Relációs adatmodell

Eddíg a zár csak 1 adaton van. Ezek az implicit zárak.

Fa protokol

Fa protokol: Egyszerű zárakat követ, melyről annyit kell tudni, hogy a T tranzakció az 1. zárját akárhova elhelyezheti, de további zárat csak akkor, ha a szülőn már van és 1 adategységet csak 1-szer zárolhat. Egyszerű feltételek:
Tétel: A fa protokol szabályait követő legális ütemezések sorosíthatóak.
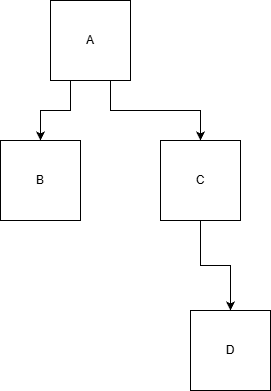Bizonyítás: Fogni kell a sorosítási gráfot, topológikusan kell rendezni majd be kell látni, hogy a rendezés ekvivalens a hierarchikus gráffal.
Tekintsük T1 és T2 1. lockjait: 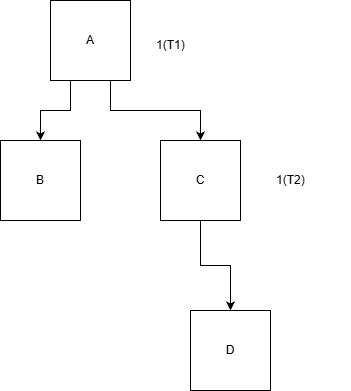Ekkor D-hez csak T1 akkor férhet hozzá, ha T2 már elengedte a szülőjét.
Ekkor T2->T1

Figyelmeztető protokol

Egy adott adategységen egy zár az összes leszármozottat is zárolja.
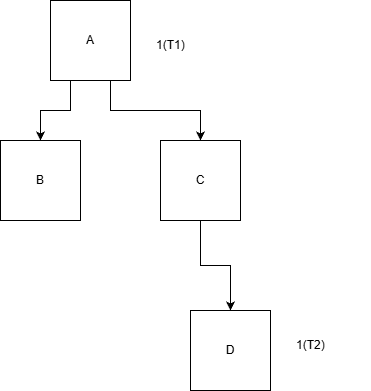Itt látható, hogy D-n implicit zár van, mert T1 zára függ T2 zárjától, ami nem jó.
Műveletei:

• LOCK A: A gyerekein az adategységnek már nem lehet se zárat, se warn-t elhelyezni.
• WARN A: Csak Warn-t lehet elhelyezni gyerekeken.

1. Zárművelet: LOCK Gyökér vagy WARN Gyökér.
2. Ezek után már akármit csak akkor lehet elhelyezni, ha a szülőn van valami.
3. Zárat akkor lehet felszabadítani ha a gyerekeken nincs lock vagy warning.
4. 2-fázisúnak kell lennie.
Tétel: A figyelmeztető protokolt betartó ütemezések sorosíthatóak és konfliktusmentesek.
Bizonyítás: TFH van zár konfliktus. Ez 2 okból lehet, T1 ősére T2 zárat akar elhelyezni. Ebből az kell, hogy az összes köztes csomóponton warn-t kell raknia, de a gyökeret T1 lockolta így ez lehetetlen. A második eset ugyanez csak T2 hamarabb helyezte el a zárat.

Mit lehet kezdeni a tranzakciók idő előtti befejezésével?

Attól fog függeni, hogy mi okozza a befejeződés?:

• User abortion.
• Hiba.
• Sorosítási feltétel VAGY patt feloldása érdekében az ütemező kilövi.
• Rendszerhiba: Csak az operatív tár sérül, háttértár sértetlen.
• Média: Csak az háttértár tár sérül, operatív sértetlen.

Médiahiba

Ezzel nem sokat tudunk csinálni. A diszkek többszörösítését lehet csinálni.

Tranzakcióhiba

Ez erős sorosítási feltételek mellett megszűnik.
Commit pont: Az az időpont amikor a tranzakció minden zárját megkapta és minden műveletét elvégezte. Ekkor már nem szakadhat meg definició szerint. Ez miért fontos? Azért, mert a vannak ABORT problémák: Dirty read.
A piszkos adat nagyon káros, mert kaszkádosítva is előfordulhat és T3 T2-n keresztül olvassa T1 piszkos adatát.
Számos sok tranzakciót kell törölni ennek a hatására. Lavina hatás: Rengeteg egymásra épülő már lefutott tranzakció törlését jelenti. Ez performance heavy. Lavinák előfordulása kerülendő: Ne olvassunk COMMIT előtt és ne írjanak a tranzakciók a COMMIT előtt.
A lavinákat iteráltan is fel lehet számolni. Ez nem annyira jó, de ezt is lehet csinálni.
Szigorú protokol: Ha egy protokol teljesíti azt, hogy az adatbázisba nem ír a tranzakció a commit előtt akkor szigorúnak nevezzük. Szigorú 2 fázisú protokol: Az összes lock a commit pont előtt van, utána írás van a db-be és utána felszabadítjuk a zárakat. Szigorú, mert teljesül, hogy commit után írunk. Tétel: Szigorú 2PL sorosítható és lavinamentes.
Bizonyítás: Szigorú->Elégséges a piszkos adat szűrésére -> Lavina elkerülésére, 2 Fázisú -> Sorosítható.
Fontos a késleltetés minimalizálása és a tranzakciós teljesítmény maximalizálása.
Tranzakciós teljesítmény: A sikeres tranzakciók lefutására fordított idő. Ezek okoznak veszteséget:

• A zárak kezelése csökkenti a tranzakciós teljesítményt.
• A tranzakció abortálás is csökkenti a futási teljesítményt.
• Következményes / Lavina felszámolása.

Konzervatív protokol: Ha sok időt fordít a tranzakciós lefutásának optimalizálására. Agresszív protokol: Ha sok időt fordít a késleltetés optimalizálására. Pl: Nagyon konzervatív protokol, ha a futás elején az összes zárat elkér egy tranzakció. Ha szüksége van egy zárt adatra akkor várakozási sorba kerül. Lehet ez egy 2 fázisú PL is.

Ekkor ez pattmentes, éhezésmentes, sorosítható, szigorú. Sok energia a betartásra de futási teljesítményt nem veszítünk.
Pl: Aggresszív protokol lehet az, hogy a legrövidebb időre kéri el a zárat.

Rendszerhibák kezelése

Az ilyen hibák ellen naplózással védekezünk.
A tranzakciókat kell naplózni, és ezeknek a műveleteit.
Egy napló rekordot a művelet végrehajtása előtt kell rögzíteni. Napló rekord: Benne van: A tranzakció mit csinált milyen adaton és mikor csinálta és mi lett az új érték. Ezen felül a tranzakció azonosító is benne lehet. A napló is blokkokból áll, ami elsődlegesen az operatív tárba íródik, majd ha megtellik, akkor a háttértárba íródik.
Ennek használata hatékonyságnövekedést is jelent.
(Amit ki lehet olvasni az adatbázisból, azt a naplóból is lehet olvasni)
Redo protokol: Szigorú 2PL + naplózás. Ha egy szigorú protokol, akkor nem lehetnek lavinák így nem kell UNDO-zni, csak REDO-zni. Időbélyeg: Megkapja egy adat azt, hogy egy tranzakció mikor olvasta utoljára. (Missed Read /Write baj lesz). Ha időbélyek szerint sorba állítjuk a tranzakciókat, akkor egy szabályos soros ekvivalenst kapunk. Csak ehhez hasonló ütemezések a helyesek. Példa: Időbélyegre, R(A) és W(A) read és write időbélyeg jelzés.

• Ha a tranzakciók már írták / olvasták akkor ezek után írható egy tranzakció és olvasható is.
• Ha a múltban akarjuk írni de már olvasták a jövőben akkor nem szabad engedélyezni a műveletet. Abortálni kell a tranzakciót. Ha írni akar akkor is. (Ha későbbi olvasás időbélyege van rajta akkor nem resetelhetjük hamarabbi időbélyegre)
• Ha időben vissza akarunk írni valamit amit már olvastunk (nagyobb az olvasási időbélyeg) akkor abortálni kell a tranzakciót. Ha olvasni akar akkor engedhetjük.

Mit lehet a lavinák ellen tenni?
Szigorú protokollokkal!

De a tranzakció időbélyeg tesztelésének atominak kell lennie különben anomáliák fordulnak elő!
Egy tranzakció commint point-ja előtt lesz az időbélyeg vizsgálata és utána az írása lesz. DE ekkor lehet más művelet a 2 művelet között, ami ellentmondás.
Ezt úgy tudjuk orvosolni, hogy zárakat helyezünk el az időbélyegre.

Verziókezeléses időbélyegek (MVCC)

Egy adat elem értékéből amikor írjuk akkor új verziót hozunk létre, hogy a régi readek a régi értékkel dolgozhassanak.
Ha a tranzakció egy későbbi olvasás/ír időbélyeget lát akkor baj van, de ha minden múlt beli elem létezik a jó időbélyegekkel akkor semmi baj nincs. Ekkor nem kell semmit sem csinálni csak elő kell venni a régi elem régi verzióját a megfelelő időbélyeggel.
Ez nem azt jelenti, hogy minden abort-tól megkímélhetjük az adatbázist, pl: az idő előtti írás majd utána már olvasást nem tudjuk engedélyezni.